Re - bonjour,

D'accord avec tes réponses à la question b

Pour répondre à la question c, tu as de nombreuses possibilités :
. avec une construction bien faite à la première question, tu peux déjà donner toutes les réponses ; on attend normalement plus d'un élève de première, surtout si l'énoncé ne prévoit pas que les réponses soient données à partir de la figure.
. la manière la plus simple est d'appliquer une relation de conjugaison qu'il faut absolument que tu saches utiliser
. bien sûr il est possible de passer beaucoup de temps avec Thalès ou les triangles semblables ; les résultats seront les mêmes. Mais la relation de conjugaison a elle-même été démontrée avec ces propriétés géométriques pour qu'ensuite on trouve plus rapidement le résultat.

Alors : peux-tu me donner des résultats (provisoires, ils seront confirmés par le calcul ensuite) simplement en lisant une figure bien faite de la première question ?

D'abord j'ai pris pour échelle
1cm 2m
AB = 2m
d = 3m
OF = 2m
la relation de conjugaison s'agissant d'une LC c'est
1/OA' - 1/OA = 1/OF'

J'avoue ne pas comprendre ton échelle...

Dans l'énoncé on a bien f = 1 centimètre ?, h = 1 centimètre ? d = 1,5 centimètre ?

Tu n'as pas une feuille de papier de 5 mètres de large ? ?

Relation de conjugaison pour une lentille mince de centre O, relation dite de Descartes
Le pied de l'objet est en A
Le pied de l'image est en A'
Le foyer image est en F'
L'axe optique est orienté (dans le sens de propagation de la lumière)



Pour cet exercice, nous allons systématiquement employer les mesures algébriques des segments et non pas leurs longueurs.

D'accord j'ai fait une erreur je reprends
AB = 1cm = 0,01 m
OF = 1cm = 0,01 m
d = 1,5cm = 0,015 m

La relation conjuguée me donne 1/OA' - 1/OA = 1/OF'
est ce que je peux continuer si c'est bon

D'accord

Que valent, avec leur signe, les mesures algébriques suivantes :





Ce sont des valeurs de l'énoncé, qu'il suffit de bien transformer en mesures algébriques (et n'oublie pas l'unité pour chacune).

est inférieur à 0 car l'objet réel est à gauche de la lentille
Ainsi est supérieur à 0
est inférieur à 0

Je suis tout à fait d'accord.

Je reste étonné par les valeurs de l'énoncé. Mais bon... Ce que je te demandais :





Es-tu d'accord avec cela ?

Si oui, quelle mesure algébrique trouves-tu pour (avec le signe est l'unité, merci) d'après ta figure ?
Et quel serait le grandissement (avec son signe) ?

= -0,01 m
= 0,01 m
= - 0,015 m

D'accord.

Que vaut d'après la figure que tu as faite pour la première question ?

Et quel est, toujours d'après cette figure, le grandissement (avec son signe) ?

Nous verrons ensuite comment confirmer ces estimations avec la relation de Descartes.

Moi je croyais qu'on devait convertir en mètre
= 1,5 cm

= OA'/OA
= 0,01/-0,01 = -1

C'est une très bonne habitude de toujours travailler avec des mètres en optique. Mais ce n'est pas obligatoire. On va continuer avec des mètres puisque tu le préfères.

Sur ma figure je ne trouve pas cela du tout...

Et quel serait le grandissement ?

Vu ta réponse à 14 h 48.

C'est cohérent (même si c'est faux)
__________

Alors, passons à la relation de Descartes.



Tu connais




Que vaut donc ?

sur ma figure j'ai = 2,5
OA'/OA = 2,5/-1,5 = -1,7

j'avais pas vu votre poste je reprends mes calculs vous corrigez

Ta réponse de 14 h 57

C'est faux mais c'est bien.
Je m'explique : tu verras bientôt que ce ne sont pas les bonnes valeurs que tu vas déterminer en utilisant la relation de Descartes.
Mais avec une toute petite figure, il y a des erreurs ; c'est difficilement évitable. Ce n'est pas grave.

Allez, on passe au calcul !

est ce que je peux faire ceci
1/ - 1/ = 1/
1/ - 1/-0,015 = 1
1/ = 1 - 1/0,015
est ce juste jusque là

1/ n'est pas égal à 1 si tu décides d'utiliser le mètre comme unité de longueur.

= + 0,01 m

et donc

1/ = 1 / 0,01

D'autre part on ne cherche pas ; on cherche

C'est une erreur mais ce que je trouve sur ma calculatrice me semble bizarre
1/ = 1/0,01 - 1/0,015
1 = (0,015 + 0,01)/ 0,01 x 0,015 0,0375

1/ = 0,0375

À peu près illisible.

S'il te plaît :

= (un signe) (une valeur numérique) (une unité)

pour que je puisse comprendre.

= 0,0375 m

C'est faux, et je ne vois pas comment tu as trouvé cela.









...

Voilà ce que j'ai fait

1/ = ( 1 / 0,01 ) + ( 1 / 0,015 )
1 / = ( 0,01 + 0,015 ) / ( 0,01 x 0,015 )

Tu vois bien :
. qu'il y a une erreur de signe
. et d'autre part il y a une erreur de calcul...

je comprends un peu mieux,

1/ = ( 0,01 - 0,015) / (0,01 x 0,015) = -33,3

1/ = 33,3

C'est dur, vraiment.
La soustraction de deux fractions !

1/ = ( 0,015 - 0,01) / (0,01 x 0,015) = + 33,3

Mais 1/ ne m'intéresse pas.

S'il te plaît :

= (un signe) (une valeur numérique) (une unité)

= 0,030 m ou 3 cm

Et que vaut le grandissement ?

Je dois d'abord chercher la taille de l'image n'est ce pas
je fais
A'B' / AB = AO'/ AO = A'B' / 1 = 3/1,5
A'B' = 3/1,5
A'B' = 2 cm ou 0,02 m

= A'B' /AB = OA' /OA = -2
je dois avoir cours tout à l'heure, je reprends demain.....

Il n'était pas nécessaire de commencer par calculer la taille de l'image.

Puisque
et que tu sais que

= -0,015 m
et que
= +0,030 m

Alors le gandissement vaut = - 2 fois
__________

La figure que j'ai faite :



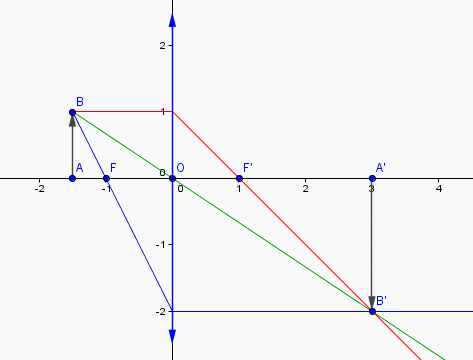
On y trouve tous les résultats !

Bonjour Coll
Merci pour tout l'aide que vous ne cessez de m'apporter et pour ces explications si importantes pour moi...
Bonne journée à tous

Je t'en prie.
À une prochaine fois !