bonjour à tous ! J'ai un problème, je ne comprends pas très bien la dernière question :

La lentille convergente est un système optique permettant de focaliser dans des rayons lumineux en un point appelé foyer après sa traversée .
On appelle O le centre de la lentille, F et F'ses foyers objet et image et f'= sa distance focal.
Le but de nombreuses expériences est la détermination de la distance focale ou de la vergence C de la lentille.

a) Rappeler la relation entre C et f'
C=1/f'
b)Soit A un point d'un objet réel AB perpendiculaire à l'axe optique orienté et situé en avant de F' et A'B' sont image donné par la lentille.
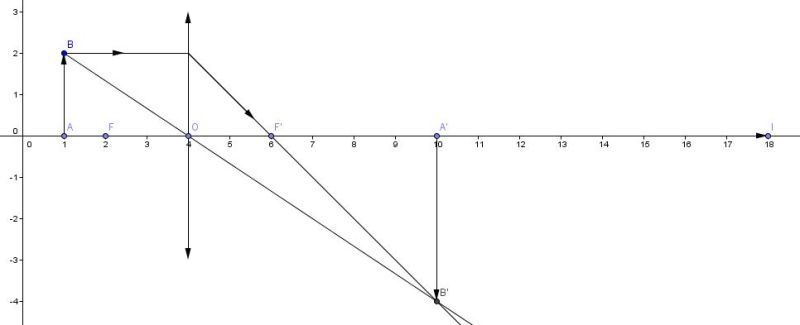
Construire proprement la position de l'image et donner ses caractéristiques (on utilisera un lentille symbolisée)
L'image est réel, renverser et plus grande que l'objet.

c) A l'aide de votre figure et en utilisant la trigonométrie, notamment les triangles F'A'B' et F'OI où I est l'intersection du rayon parallèle à l'axe optique et du plan de la lentille, retrouver la relation de conjugaison de René Descartes entre , et f'

Je ne comprends la question c), enfin comment faire. Merci d'avance