Inscription / Connexion Nouveau Sujet
Lentille convergente
Bonjour, il y a deux questions dans un exercice où je bloque.
Énoncé : On utilise une lentille convergente pour réaliser l'image A'B' d'un objet de AB de 2.0 cm sur un écran. L'image, de 8 mm, est située à 12.0 cm de l'objet et est inversée.
1) Calculer le grandissement y.
Ma réponse : y = -A'B'/AB = -0.8/2.0 = -0.4
2) Faire un schéma à l'échelle 1/1 sur lequel figure l'axe optique, la lentille, l'objet AB et l'image A'B'.
Là je bloque car je ne comprends pas à quelle distance du centre optique il faut placer l'objet et l'image
3) Dessiner les trois rayons particuliers permettant de trouver la position de l'image A'B' de l'objet AB. Construire l'image A'B' de l'objet AB.
Là je bloque aussi
Quelqu'un peut m'aider svp 
Bonjour,
La deuxième question suit toujours la première...
Maintenant que tu connais le grandissement, et que l'énoncé te donne la distance tu devrais pouvoir déterminer toutes les distances...

Tu es bien silencieux(-se)...
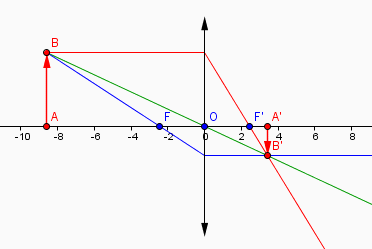
Que penses-tu de ce schéma ?
Les échelles selon l'axe optique et perpendiculairement à cet axe ne sont pas du tout identiques.
Mais :
. le grandissement vaut -0,4
. la distance AA' vaut 12 cm

Il y a trois rayons particuliers qui sont utilisés pour construire une image à partir d'un objet.
L'un de ces trois rayons est celui qui passe par le centre optique O de la lentille : il a ceci de particulier qu'il n'est pas dévié au passage de la lentille.
Donc :
. tu traces un axe optique
. tu places le point A
. tu traces l'objet de 2,0 cm de hauteur : AB
. tu places le point A' à 12 cm du point A
. tu traces l'image A'B' de 8 mm de hauteur et qui est renversée par rapport à l'objet
. le segment de ligne droite BB' est le rayon qui n'est pas dévié par la lentille
Conclusion : le point O d'intersection de ce rayon BB' et de l'axe optique AA' est le centre optique de la lentille.

Parviens-tu à tracer maintenant les trois rayons ? Il y en a déjà un qui est tracé. Il faut tracer les deux autres :
. celui qui part de B et qui est parallèle à l'axe optique : il passera par le foyer image après la lentille !
. celui qui arrive en B' en étant parallèle à l'axe optique : il est passé par le foyer objet avant la lentille !

Travaille bien cet exercice. Quand tu sauras sans hésiter tracer ces trois rayons tu sauras à peu près tout de l'optique géométrique telle qu'on l'enseigne au lycée !

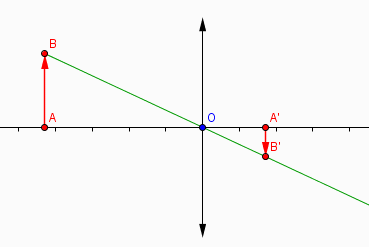
Je reviens car je suis actuellement en train de faire mon schéma & j'ai un problème,
J'ai bien tracé mon axe optique, mon objet AB de 2.0 cm de hauteur et mon image A'B' de 8 mm de hauteur située à 12 cm de mon objet.
Mais quand je veux tracé mon 1er rayon passant par le centre optique O, ça ne marche pas 
Qu'est-ce qui ne marche pas ?
As-tu dessiné l'image A'B' renversée par rapport à l'objet AB ?
Tu dois simplement avoir (avec des dimensions différentes) une figure qui ressemble beaucoup à ce que j'ai posté à 16 h 40

Oui, j'ai fait la même chose que sur votre schéma.
Le rayon qui va du point B et qui passe par le centre optique n'atteint pas le point B' et descend beaucoup plus bas.
Le rayon vert est le rayon qui joint le point B au point B'
Il coupe l'axe optique à l'emplacement du centre optique de la lentille : O
On ne connaît pas la position de ce centre O avant d'avoir fait la construction.
Relis mon message de 17 h 25

Ah oui c'est bon ça marche 
& sinon une dernière question : pour la question 4 on me demande de déterminer graphiquement la distance focale OF' donc 2.7 cm et ensuite on me demande de déduire la vergence de la lentille donc est-ce qu'il faut que je fasse C = 1 / 0.27 ?
Attention, pour calculer la vergence (en dioptries de symbole  - la lettre grecque "delta" -) il faut que la distance focale soit exprimée en mètre !
- la lettre grecque "delta" -) il faut que la distance focale soit exprimée en mètre !

Un résultat sans son unité est un résultat nul
_________
Tu trouves + 37 dioptries ou + 37 
Par le calcul je trouve une distance focale d'environ 2,45 cm et une vergence d'environ + 40,8 

Je sens que je me suis encore trompée quelque part....  Alors graphiquement, pour OF j'obtiens 2.4/2.5 et pour OF' j'obtiens 2.7
Alors graphiquement, pour OF j'obtiens 2.4/2.5 et pour OF' j'obtiens 2.7
Ce n'est pas très facile graphiquement. Il faut être très précis.
Bien sûr, tu dois avoir
Par le calcul ce n'est pas très difficile (théorème de Thalès, comme d'habitude) mais on ne te le demande pas apparemment. Je suis sûr de mes résultats...