Inscription / Connexion Nouveau Sujet
lentille convergente 1ere
Bonjour,
Un objet perpendiculaire à l'axe optique est situé à 6cm devant une lentille convergente. 1)Quelle doit etre la position de l'écran pour observer une image cinq fois plus grande que l'objet? 2)Calculer la distance focale de la lentille. Je bloque aussi pour mon 2eme exercice car mon cours me donne les formules de conjugaison et d'agrandissement mais aucun exemple d'exercice et je n'arrive pas à voir les elements du texte qui me permettent d'appliquer les formules.
Mon DM est à rendre lundi et c'est en dernier recours que je m'adresse à vous, merci à vous de m'aider, cela fait 2 soirs que je me couche à 1h30 pour essayer de trouver une solution, je suis sure qu'il ne manque pas grand chose car je sais calculer une distance focale, une position mais je n'arrive pas à interpreter les éléments qui me sont donnés. Le renseignement de l'image cinsq fois plus frande doit servir à queque chose.
Bonjour baboune1,
pas de panique ce n'est pas compliqué. Comme toujours en optique géométrique, on peut trouver la solution soit avec une construction, soit avec l'algèbre.
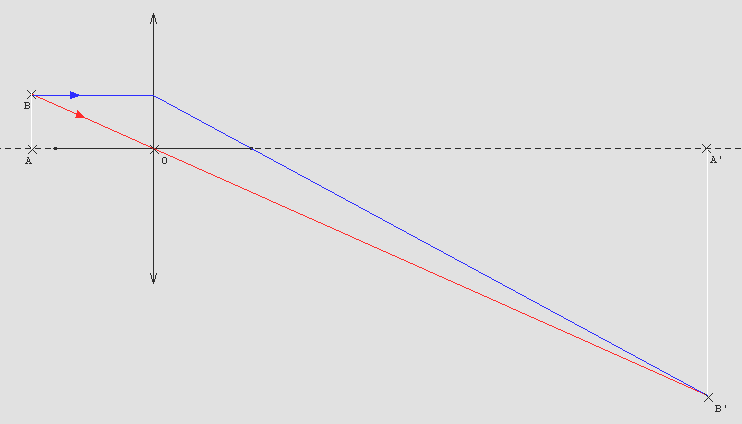
I - Voici d'abord la construction, regarde le schéma ci-dessous ; comme il est achevé, je t'explique comment s'y prendre et je te conseille de le refaire à l'échelle sur du papier quadrillé :
a) tu dessines un axe optique et une lentille convergente, sans placer les foyers puisque tu ne les connais pas. Tu places un objet A sur l'axe à 6cm devant O, puis un point B au-dessus de A (pas trop loin car l'image de AB va être agrandie 5 fois...). Tu mesures la distance AB, par exemple 1 cm.
b) Tu traces BO que tu prolonges (rayon rouge sur mon dessin) : ce rayon lumineux passe par le centre optique de la lentille, donc il continue en ligne droite. Il est essentiel que tu comprennes que l'image B' de B se trouve sur ce rayon. Il ne reste plus qu'à trouver, sur le rayon émergent rouge, le point B' qui se trouve à la distance 5AB de l'axe optique (avec mon exemple, à 5 cm). Tu rabaisses alors B' sur l'axe pour obtenir A', image de A.
Le théorème de Thalès t'indiquera tout de suite qu'on obtient OA' = 5.OA, sans tenir compte des signes.
c) Pour faire apparaître les foyers de la lentille, il suffit maintenant de tracer un rayon issu de B et parallèle à l'axe optique (bleu sur mon dessin). Par définition, le rayon émergent va passer par le foyer image F', et bien entendu il passe aussi par B'. L'intersection de l'émergent bleu avec l'axe optique te donne le foyer image F' de la lentille, dont tu déduis la distance focale OF' = f'. Vu ?
Si tu fais cette construction à l'échelle tu dois trouver OF' = 6 cm.
II - Voici maintenant le raisonnement algébrique. Pour simplifier les notations je pose mesure algébrique de OA = p, mesure algébrique de OA' = p', mesure algébrique de OF' = f'. On gagne un temps fou en ne plaçant pas la barre de mesure algébrique...
Ici, on a p = - 6 cm (négatif car A est devant la lentille), p' > 0 (image sur un écran donc à droite de O).
Quant au grandissement, il est connu puisque sa valeur absolue vaut 5 (image 5 fois plus grande) et il est négatif (image sur un écran donc renversée). OK ?
Les relations que tu connais s'écrivent alors -1/p + 1/p' = 1/f', et pour le grandissement 
= p'/p.
Le calcul est classique : je connais p et donc je vais éliminer p', en écrivant p' = p et en reportant dans la relation de conjugaison :
-1/p + 1/(p) = 1/f' = (1/p).(1: - 1), ce qui donne facilement f' = p./(1 - ).
En faisant p = -6 cm et = -5, ça ne m'étonnerait pas que tu obtiennes f' = 5 cm...
Si tu as des questions n'hésite pas. En revanche je n'aurai pas le temps de corriger ton exercice sur la loupe, du moins pas avant 18h, mais d'ici-là tu auras sûrement un autre correcteur qui va s'y coller.
Annuler
connectez vous