Bonjour quand même...

Dans le référentiel géocentrique, quelle est la vitesse angulaire du satellite ?
Quelle est la vitesse angulaire de la Terre dans ce même référentiel ?

Quand le satellite se retrouve pour la première fois à la verticale d'un même lieu, la Terre a tourné d'un angle que l'on peut appeler . De quel angle a tourné le satellite ?

je sais pas

Dans le référentiel géocentrique, la vitesse angulaire du satellite est 2/4.16*10^-4
donc la vitesse angulaire de la Terre dans ce même référentiel est 2/4.16*10^-4.

Quand le satellite se retrouve pour la première fois à la verticale d'un même lieu, la Terre a tourné d'un angle que l'on peut appeler . De quel angle a tourné le satellite ?
je ne sais pas.

aidez moi svp

Je ne comprends pas. Peux-tu m'expliquer d'où vient 4,16.10^-4 ?

excusez moi c'est 2/5400

aidez moi svp

aidez moi SVP

Dans le référentiel géocentrique, le rayon qui va du centre de la Terre, origine du référentiel, au satellite fait un angle de 2 radians (un tour) en 5 400 secondes
Quelle est la vitesse angulaire du satellite dans ce référentiel ?

2/5400

Oui, quelle est l'unité ?

La Terre fait un tour sur elle-même dans un référentiel géocentrique en 23 h 56 min et 4 s
quelle est la vitesse angulaire de la Terre ?

2/86164

c'est bon ou pas

Je t'ai demandé d'indiquer les unités.

radians par seconde

aidez moi svp

Une figure :



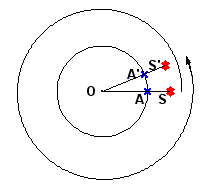
O est le centre de la Terre.
Pour t = 0 le satellite est en S à la verticale au-dessus du point A

Pour t = t' la Terre a tourné. Le point A est maintenant en A'. Le satellite a tourné autour de la Terre à une vitesse angulaire beaucoup plus importante que celle de la Terre. Il se retrouve en S' qui est à la verticale du point A'

Exprime l'angle dont la Terre a tourné (l'angle ) en fonction de la vitesse angulaire de la Terre et de la durée recherchée t'

Exprime aussi l'angle dont le satellite a tourné en fonction de la vitesse angulaire du satellite et de la même durée t'

Que vaut (en radians) l'angle par rapport à l'angle ?

Ceci te donne l'équation qui te permet de trouver t'

je n'arrive pas comprendre votre schéma.

Qu'est-ce que tu ne comprends pas ?

comment on peut trouver l'angle AOA'

Tu as calculé la vitesse angulaire de la Terre
On dit simplement que l'angle est l'angle dont tourne la Terre pendant le temps t' que l'on ne connaît pas mais que l'on va trouver par une équation. Tu as déjà fait de l'algèbre...

donc l'angle AOA'= 2t'/86164 radians

Calcule de même l'angle

l'angle SOS' = l'angle AOA'

Le satellite a fait un tour de la Terre avant de survoler à nouveau le point A

donc l'angle SOS'=4t'/86164 radians

Pourquoi 4 ? Pourquoi une période qui est celle de la Terre et pas celle du satellite ?

1) Reprends la vitesse angulaire du satellite (pas celle de la Terre)
2) exprime l'angle correspondant à cette vitesse angulaire pour une durée t'

ah oui, excusez moi l'angle SOS' = 2t'/5400

Oui !

Reprends la figure et dis quelle est la différence (en radians) des mesures des angles et

W Terre = 2Pi/(24*3600) rad /s

w Satellite = 2Pi/(1,5*3600) rad /s

Angle parcouru Terre = [2Pi/(24*3600)] t

Angle parcouru Satellite = [2Pi/(1,5*3600)] t

Le Satellite repasse à la verticale d'un même lieu si :

Angle parcouru Satellite = Angle parcouru Satellite + 2kPi (k dans N)

[2Pi/(1,5*3600)] t = [2Pi/(24*3600)] t + 2kPi

Repasse pour la première fois pour k = 1 -->

[2Pi/(1,5*3600)] t = [2Pi/(24*3600)] t + 2.Pi

[1/(1,5*3600)] t = [1/(24*3600)] t + 1

[1/(1,5*3600) - (1/(24*3600))] t = 1

(1/1,5 - 1/24) t = 3600

(16/24 - 1/24) t = 3600

t = 3600 * 24/15 = 5760 s
-----
Sauf distraction.  

il n'ya pas de différence les 2 angles sont egaux.

Bonjour J-P
C'est très bien !
t' = 5 761 s en calculant avec la période de révolution sidérale de la Terre (comme quoi, on s'embête parfois pour pas grand-chose...)

raja >>
Je t'ai déjà répondu à 9 h 10 que cette réponse n'est pas bonne car le satellite a fait un tour de la Terre avant de revenir à la verticale du point A

Salut Coll

l'angle AOA'=SOS'+2

Puisque c'est le satellite qui fait un tour de plus

SOS' = 2 + AOA'

Tu as tout ce qu'il faut maintenant :

2t'/5400 = 2 + (2t'/86 164)

Simplifie par 2

Résous l'équation et tu trouves t'

ok merci

Je t'en prie. Donne ton résultat... on ne sait jamais

bonjour
en 1 heure, le point sur la terre fait 1/24 de tour
le satellite fait 1/1.5 = 2/3 de tour
il rattrape 2/3 - 1/24 = 16/24 - 1/24 + 15/24 de tour
le satellite reviendra au-dessus du point aorès 1/(15/24) = 24/15 heure = 24*4 minutes = 96 minutes = 1 heures 36 minutes

Bonjour,

Ah, la vieille école... la belle époque de l'arithmétique ! Je pense que c'est loin des possibilités de raja

je trouve t=5761,05 s

Bravo raja !

Tu t'es bien accroché à ce problème ; c'est ainsi que tu progresseras.

On ne va pas laisser la durée sous cette forme
5761 secondes ce sont 1 heure 36 minutes et 1 seconde
Avec les symboles corrects : 1 h 36 min 1 s

merci a+

Je t'en prie.
A une prochaine fois !