Inscription / Connexion Nouveau Sujet
le pendule simple
Bonjour,
Je n'arrive pas à résoudre cet exercice qui je pense, pourrait m'être bien utile pour l'évaluation qui aura lieu juste après les vacances.
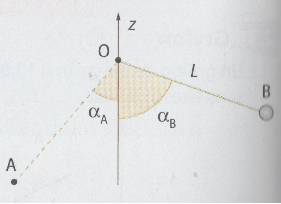
II] Considérons le pendule du professeur Tournesol des albums de tintin. On l'incline d'un angle αA par rapport à la verticale et on le lance à la vitesse VA =1,0m/s. Il arrive en B avec une vitesse nulle.
Données :
Longueur du pendule : L=20cm ; αA =30° Les frottements sont négligeables.
Au point O, EPP(O) = 0J.
1) a. Déterminer l'expression des altitudes en A et B, ZA et ZB, en fonction de L et respectivement αA et αB.
b. En déduire les expressions des énergies potentielles de pesanteur du pendule en A et B.
2) a. Donner les expressions des énergies mécaniques du pendule en A et B.
b. En déduire l'expression de l'angle maximum αB atteint par le pendule. Calculer sa valeur.
Merci d'avance pour vos réponses.
Bonjour,
Le problème commence à la question 1.a et la 2.a ce qui m'empeche de faire les autres.
Je ne crois pas connaitre de formule me permmetant de calculer la hauteur de point A ou B. :s
As-tu fait une figure ?
Sur celle que j'ai faite, le pendule est accroché à un point O et la masse à l'extrémité du fil, initialement en A, peut atteindre B en passant par un point bas C à l'aplomb de O.
Soit H et K les projetés orthogonaux de A et B sur OC.
La hauteur du point A au-dessus du point bas est HC et celle du point B est KC.
OH peut être calculé dans le triangle 0AH où OA et l'angle HOA sont connus. D'où HC.
bonjour,
Il y a en effet un dessin sur le livre mais que je n'est pas mis (je vais essayer de le mettre).
Je n'avais pas pensé à faire un triangle pour trouver la hauteur car je cherchais plutôt l'expression littérale qui permmetterai de trouver Za et Zb.
Je vais donc tenter de trouver la formule a partir de l'aide que vous m'avez fourni.
Merci.
Bonjour,
Pour la 1) a je trouve:
Za= 20-(cos( a)*20) et Zb = 20-(cos(
a)*20) et Zb = 20-(cos( b)*20)
b)*20)
Pour la 1)b:
EPa = m.g.ZA <=> EPa = m.g.(20-(cos( a)*20))
a)*20))
EPb = m.g.ZB <=> EPb = m.g.(20-(cos( b)*20))
b)*20))
Je pense avoir bon mais il me reste la 2 a et b que je ne trouve pas.
2 a) Il faut ajouter les énergies cinétiques aux énergies potentielles.
En A, la masse pesante a une vitesse VA qui lui a été communiquée au départ.
En B, la masse pesante s'arrête et sa vitesse est nulle.
Bonsoir,
Ema = Epa+Eca
Ema= 26.48*m+1/2*m
Ema= (53.96/2)*m
Pareil pour Emb je pense.
Plus que la 2)b
Or, le fait qu'il n'y ai pas de masse donnée ne poserai-t-il pas problème?
Bonjour,
J'ai le même exercice à faire.
Sauf que je ne comprends pas ton raisonnement pour la 1.a).
Si quelqu'un peut m'expliquer svp. Merci d'avance.
1 a) Za et Zb sont les différences de hauteur entre les points extrêmes A et B et le point bas de la trajectoire circulaire de la masse pesante.
Qu'est-ce que tu ne comprends pas ?
Bonjour,
Je sais que ce sujet date un peu mais j 'aimerais que l' on m'explique sil vous plaît! Merci
Je n'ai pas trop compris pour pourquoi pour la question 1)a
za=20-(cos(x)*20)
ça devrait pas être ça ?
cos  a=adj/hyp
a=adj/hyp  cos
cos  a=Za/L
a=Za/L
cos  a*L=Zb
a*L=Zb
Rebonjour,
Alors voilà j' ai le même exercice à faire pour la rentré mais comme j 'ai pas trop compris même avec l 'aide fournir à dylan1 je ne comprends toujours pas quelqu'un pourrais l'aider sil vous plâit ?
Alors voilà pour la question 2)a de de dylan1 mes résultats ne sont pas les même
voilà ce que moi j' ai trouvé:
Ema=Eca+Eppa=1/2*m*v²+m*9.8*20-(cos(30)*20)
=1/2*m+192.91*m=m(192.91+1/2)
(c'est pas bon ??)