Inscription / Connexion Nouveau Sujet
Le pendule qui bat a seconde
Bonjour,
j'ai un exercice de physique sur lequel je bloque.
Je vous remercie d'avance de votre aide. Voici l'énoncé et mes réponses que vous voudrez bien corriger au besoin :
un pendule simple est constitué d'une bille de masse m, suspendue à un fil rigide de longueur l dont la masse est négligeable. Si l'on écarte le pendule de sa position de repos, il se met à osciller . Un aller et retour constitue une oscillation, et sa durée est une période T, qui peut se mesurer en seconde.
Afin de réaliser un pendule dont la période est d'une seconde, un groupe d'élèves mesure 10 périodes en faisant varier la masse m de la bille, puis la longueur l du fil.
Expérience 1, pour l = 50cm
m(g) 50 100 150 200
10T(s) 14.1 14.1 14.0 14.2
Expérience 2 pour m=100g
l(cm) 25 35 45 60
10T(s) 10.1 12.0 13.5 15.5
1) a) pourquoi mesurer 10 périodes et non une seule ?
je réponds : on mesure 10 périodes et non une seule pour avoir la période d'oscillation du pendule de manière plus précise en faisant une moyenne.
b) Comment calculer la période pour chaque série de mesures ?
Je réponds : on note dans chaque série toutes les mesures une à une jusqu'à 10 mesures et ensuite on divise la somme de ces mesures par 10 pour avoir une moyenne.
2) Que peut-on en déduire quant à l'influence de la masse sur la période du pendule ?
Je réponds que la période T du pendule ne varie quasiment pas donc la masse n'a pas d'influence sur la période du pendule.
3) La longueur du fil a t elle une influence sur la valeur de la période ?
Je réponds : oui la longueur du fil influe sur la valeur de la période car plus la longueur du fil est importante et plus la durée de la période augmente.
4) Pour une période d'une seconde, quel est l'ordre de grandeur de la longueur l à utiliser ?
Je réponds : l'ordre de grandeur de la longueur l à utiliser est de 25cm.
5) Pour vérifier si la période T est proportionnelle à la longueur l, tracer les deux graphiques suivants : T en fonction de l et T en fonction de racine carré de l.
a) Quel est le graphique le plus simple à exploiter ?
b) En déduire une relation entre T et l.
c)le professeur du groupe propose la relation suivante : T=2pi racine carrée l/g avec g=9.8N.kg exposant -1(intensité de pesanteur sur la Terre).
Vérifier si la relation trouvée à la 5b)est cohérente avec cette expression.
d) calculer la longueur exacte de l pour que la période soit d'une seconde.
Pour tout le 5) je suis perdue et j'ai vraiment besoin de votre aide.
Merci beaucoup pour vos prochaines réponses
Bonjour,
Ce n'est pas un pendule qui bat la seconde mais c'est un pendule dont la période vaut 1 seconde.
Un pendule qui bat la seconde est un pendule dont la période vaut 2 secondes (et la longueur nécessaire pour le pendule simple correspondant est d'environ 1 mètre)
Mais si tu as choisi ce titre c'est qu'il t'est donné par le livre ou le polycopié. Tu n'y es pour rien... mais c'est faux quand même !
__________
1a) : oui
1b) : on mesure 10 périodes et on note la durée de ces 10 périodes. On divise cette valeur par 10 pour avoir la durée d'une période
2) : oui
3) : oui
4) : oui
Question 5a :
pour T en fonction de l :
| Longueur l (m) | 0,25 | 0,35 | 0,45 | 0,50 | 0,60 |
| Période T (s) | 1,01 | 1,20 | 1,35 | 1,41 | 1,55 |
et pour T en fonction de
 l
l l ( l ( m) m) | |||||
| Période T (s) | 1,01 | 1,20 | 1,35 | 1,41 | 1,55 |
Il faut remplir la première ligne (ou au moins me donner les valeurs et je remplirai le tableau si tu ne sais pas le faire) du deuxième tableau et tracer les deux graphiques.

Merci Coll pour votre aide mais je suis désolée je ne sais tellement pas ou je dois aller que je ne sais pas répondre à votre demande qui est de remplir la première ligne en mettant des valeurs car je ne sais pas de quelle valeurs vous parlez ??? Je suis complètement larguez et je voudrais comprendre car je déteste ça.
Désolée et encore merci pour votre aide. J'ai encore besoin de vous.
Ou est ce
Pour T en fonction de Racine carrée l
Racine carrée l 0,5 RC35/10 3RC5/10 RC2/2 RC15/5
Période T(s) 1,01 1,20 1,35 1,41 1,55
avec RC = racine carrée
Mais je ne pense pas que ce soit cela car alors comment faire un graphique avec des racines carrées en valeur ? J'ai tout simplement appliqué à racine carrée à la longueur du fil.
Merci pour votre patience.
La première est bonne.
 0,25 = 0,5
0,25 = 0,5
 l ( l ( m) m) | 0,5 | ||||
| Période T (s) | 1,01 | 1,20 | 1,35 | 1,41 | 1,55 |
Mais pourquoi n'as-tu pas continué à calculer les autres
 l ?
l ?

l (m) 0,5 0,59 0,67 0,707 0,77
Période T (s) 1,01 1,20 1,35 1,41 1,55
En fait je pensais que cela n.est pas cela c'est pourquoi je n'ai pas continué.
Pour moi, le graphique le plus simple a utilisé est le premier car plus lisible mais comment en déduire une relation entre T et l ? Je ne sais pas. Si je lis la suite de l'énoncé je pense qu'il doit y avoir un rapport mais je ne comprends pas lequel ? Merci pour vos réponses.
Très bien !
 l ( l ( m) m) | 0,500 0 | 0,591 6 | 0,670 8 | 0,707 1 | 0,775 6 |
| Période T (s) | 1,01 | 1,20 | 1,35 | 1,41 | 1,55 |
Le premier graphique ressemble à ceci :
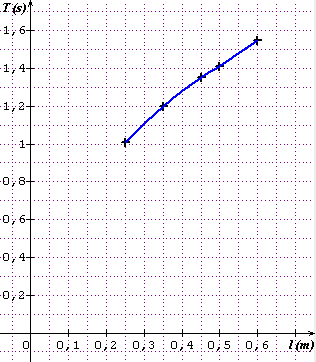
et le second ressemble à ceci :
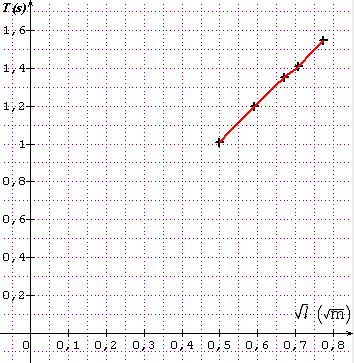
Qu'en dis-tu ?

Je trouve qu'ils sont presque pareil mais le second est plus précis.
Mais comment en déduire une relation entre T et l ? Je ne sais pas. Si je lis la suite de l'énoncé je pense qu'il doit y avoir un rapport mais je ne comprends pas lequel ? Merci pour vos réponses.
Tu as tout à fait raison de lire la suite de l'énoncé.
On ne devrait jamais commencer la première question sans avoir lu et relu plusieurs fois tout l'énoncé.
_________
5a : oui c'est le deuxième graphique qui est le plus facile à exploiter. On y reconnaît une relation linéaire : ce segment de droite s'il est prolongé donne une droite qui passe par l'origine.
5b : puisqu'il semble bien que la période soit une fonction linéaire de la racine carrée de la longueur cela signifie que
k étant un coefficient.
5c : ce qui est cohérent avec ce que le professeur propose
cela signifie que le coefficient k proposé à la question 5b est tout simplement
5d : que proposes-tu ?

Donc d'après ce que je comprends, je propose :
T=2Pi/RCg * RC l = 2,007 * RC 25 = 2,007 *5 = 10,035
Or je crois qu'on devrait être proche de 25 je ne comprends rien notamment le 5)c
Je suis nulle et je m'en excuse mais je ne percute pas. Désolée
Merci d'avance
On te donne la relation :
On veut T = 1 s
On connaît
. 2
. 
. g = 9,8 N.kg-1
On cherche , la longueur du pendule.
Il y a une simple équation à résoudre.

En fait à la 5)b) je dois répondre qu'il y a une relation de proportionnalité entre T et l et le coefficient de proportionnalité est k=2*Pi/RCg
5)c)1 = 2*Pi*RC l/9.8
????
Ton début de réponse à la question 5d : oui
Il faut en déduire la valeur de la longueur l du pendule simple dont la période vaut 1 seconde.
Tu as une équation à une seule inconnue : l

Je sais qu'il me faut uniquement résoudre mais cette racine carrée me bloque j'arrive à :
RCl = 0,51282
l=0,51282 au carré
Merci Coll pour votre précieuse aide Très bonne journée et encore mille fois merci
Donc je m'excuse je termine
l égal environ 2,5 soit 25 cm environ comme trouver au 4)
Merci a très bientôt
Merci beaucoup pour votre détail très clair contrairement à moi. Alors pour éviter toute erreur de rédaction lors de la rédaction sur ma copie j'ai noté l'égalité du départ comme je vous l'avais écrite et que vous aviez validé et comme je savais que la longueur du fil devait être de 25 cm comme répondu au 4) alors j'ai mis à peu près égal à 25 cm. On verra.
En tout cas vraiment merci pour tout vous m'avez énormément aide et tout ce que j'ai fait je l'ai compris maintenant je vais approfondir sur votre résolution d'équation car j'avoue avoir eu de mon côté du mal pour cette résolution pourtant habituellement j'aime résoudre des équations.
Merci, merci encore et encore pour cour aidé votre patience et votre temps pris pour moi. 
Qu'elle idiote je fais effectivement en mettant T au carré tout est très simple je n'y ai pas pensé. Merci et à très bientôt.



 24,8 cm
24,8 cm

