Inscription / Connexion Nouveau Sujet
Le neutrino
Bonsoir ! 
J'aurai besoin d'un micro coup de pouce pour mon DM de physique (j'essaierai de faire bref, l'énoncé est costaud), juste une petite piste pour m'aider à y voir plus clair 
On me demande d'écrire l'équation de désintégration beta - du cobalt 60.
On obtient :
6027C -> 6028Ni + 0-1e
Puis on me demande de calculer l'énergie libérée :
sachant que
masse du noyau de cobalt = 9,952238.10-26 kg
masse du noyau de nickel = 9,951734.10-26 kg
masse électron = 9,109383.10-31 kg
vitesse de la lumière = 2,99792458.108 m/s
J'obtiens une énergie libérée (valeur absolue) de 1,237862 x 10-21 J
Jusque là, pas de souci. Mais après on me demande la quantité d'énergie que le neutrino doit emporter pour que l'énergie se conserve.
Là ça coince ! je sais que l'énergie est retrouvée sous forme de rayonnement ou cinétique. Dans ce cas on m'explique dans l'énoncé que parfois l'électron émis lors de la désintégration ne reçoit pas toujours la même quantité d'énergie cinétique (elle va de 0 à 5,111.10-14 J).
Mais comment savoir la quantité d'énergie emportée par le neutrino ? :'(
Voilà, merci beaucoup pour votre aide (j'espère que j'ai réussi à tout synthétiser...), la plus petite piste serait la bienvenue 
Bonjour,
L'énergie libérée se partage entre le noyau de nickel , l'électron et l'antineutrino .
Pour le noyau , lourd et massif , la part est négligeable devant les 2 éléments restants .
Donc , l'énergie libérée se partage entre l'électron et l'antineutrino .
Bonjour, merci pour votre réponse !
Oui, j'avais compris... mais je ne vois pas quel calcul faire ! désolé, c'est sans doute très simple mais je ne vois vraiment pas...
Une soustraction !
Vous avez l'énergie libérée ( qui , je pense est fausse , c'est pourquoi vous êtes gêné ... ) , vous avez la part emmenée par l'électron en donnée , il reste la part emportée par l'antineutrino .
Je tique toujours de répondre lorsqu'il y a des données critiquables.
Voila une réponse qui remet certaines choses d'aplomb (et tant pis si elle s'écarte de ce qui est annoncé dans l'énoncé). Ce n'est pourtant pas bien difficile d'obtenir (voire calculer) des données correctes, pourquoi alors trouve-on tant d'approximations dans ces exercices d'école ?
---------
Et donc : Pour info plus que pour résoudre le problème avec ses données pour le moins imprécises.
Puisqu'on mentionne le neutrino, il me semble qu'il devrait figurer dans l'équation de désintégration (bizarre car en general le neutrino est hors programme en première et même en Terminale, me semble-t-il).
De plus, dans une désintégration Beta -, ce n'est pas un neutrino qui est généré mais un antineutrino.
6027C -> 6028Ni + 0-1e +
Delta m = 9,951734.10^-26 + 9,109383.10^-31 - 9,952238.10^-26 = -4,129.10^-30 kg
E = Delta m * c² = -4,129.10^-30 * (2,99792458.10^8)² = - 3,711.10^-13 J (soit -2,316 MeV)
Remarque : On aurait du trouver E = -2,824 Mev et pas -2,316 MeV)
On trouve cette info sur ce site : ![]()
L'erreur vient des données fausses.
Les masses données dans l'énoncé pour les noyaux des atomes sont en fait la masse des atomes(et pas des seuls noyaux)
On se retrouve alors avec une erreur sur le delta masse erronée de la masse d'un électron
----------
Pour info, je recalcule les données corrctes (pas de problèmes pour trouver les masses des atomes (voir isotopes du Nickel et isotope de Cobalt sur wiki)
Et de calculer les masses des noyaux en retirant la masses des électrons.
On a alors ceci :
Pour les atomes (complets) :
m Ni60 = 59,9307864 u = 59,9307864 * 1,660538921.10^-27 = 9,95174033833.10^-26 kg
m Co(60) = 59,9338171 u = 9,95224239187.10^-26 kg
Pour les noyaux d'atomes :
m Ni(60) = 9,95174033833.10^-26 - 28*9,109383.10^-31 = 9,94918971109.10^-26 kg
m Co(60) = 9,95224239187.10^-26 - 27*9,109383.10^-31 = 9,9497828584.10^-26 kg
Delta m = 9,94918971109.10^-26 + 9,109383.10^-31 - 9,9497828584.10^-26 = - 5,0205.10^-30 kg
E = Delta m * c² = -5,0205.10^-30 * (2,99792458.10^8)² = -4,512.10^-13 J (soit -2,82 MeV)
On trouve bien alors la valeur de E correcte pour la désintégration Beta- du Co60
-----------------------------
L'énergie produite par la désintégration se "distribue" sous différentes parties :
En énergie cinétique de la particule beta- (électron)
En énergie pour l'anti neutrino
En énergie cinétique pour le noyau fils (Ni60)
En énergie gamma car le noyau de Ni60 généré par la sésintégration est en général dans un état excité ... et il revient vers l'état stable en émettant 1 photon gamma.
En général, l'énergie cinétique est surtout transmise à l'électron, et quasi rien (en E cinétique) au noyau Ni (facile à démontrer par la conservation de la quantité de mouvement)
L'énergie pour le neutrino est aussi en général très faible
Donc, en première et bonne approximation, l'énergie produite par la désintégration se partage presque intégralement pour les photons gamma et comme E cinétique pour l'éelectron.
On voit sur ce diagramme :
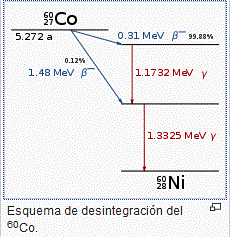
Que dans 99,88 % des cas, on a 0,31 MeV d"énergie cinétique pour la particule Beta- (électron)
et qu'il y a 2 photons gamma émis, l'un de 1,1732 MeV et l'autre de 1,3325 MeV
La somme de ces énergies, soit 0,31 + 1,1732 + 1,3325 = 2,816 MeV ... qui correspond à la presqu'intégralité de l'énergie produite par la désintégration.
Et que dans 0,12 % des cas, on a : 1,48 MeV d"énergie cinétique pour la particule Beta- (électron)
et 1 photon gamma émis de 1,3325 MeV
Ici, on a la somme de ces énergie égales à 1,48 + 1,3325 = 2,8125 MeV ... qui correspond à la presqu'intégralité de l'énergie produite par la désintégration.
-----
Rien relu ... mais comme mes résultats collent avec ce qui est annoncé sur les sites (sérieux) concernant l'énergie produite pour cette désintégration, les résultas trouvaient sont sûrement corrects. (avec ce qui se passe en réalité et pas en concordance avec l'énoncé ... cela devient assez habituel.)
--------------------------------
Voila, fais ce que tu veux avec cette réponse.

Bonjour,
La première erreur du demandeur était de trouver un delta m en 10^-21 J ...
Après , bien sûr , le résultat était un peu bancal avec 2 .316 MeV au lieu de 2.824 MeV ...
La première erreur du demandeur était de trouver un delta m en 10^-21 J ...
Ca c'est sûr.

------------
Les erreurs dues à la confusion dans l'énoncé entre les valeurs des masses d"atomes au lieu de celle des noyaux ne changent rien dans le principe de calcul, on pourrait donc dire que c'est sans importance ...
Cependant, je pense qu'il est bon, pour l'étudiant, de prendre l'habitude de recouper les résultats qu'il trouve avec les résultats de sources "sûres" ... ce qui ne peut que foirer si les données initiales fournies sont fausses.
C'est surtout pour ce motif que cela me titille toujours de trouver des erreurs de valeurs dans les énoncés, cela ne pousse pas les étudiants à avoir le bon réflexe de vérifier ce qu'ils trouvent ... par rapport à "la réalité" qui devrait être disponible sur le net... puisque cela ne colle que très rarement à cause des "erreurs" de valeurs de l'énoncé.
Il devient d'ailleurs parfois bien compliqué de trouver des données fiables, tant les erreurs des uns mises sur le web sont multi-recopiées par d'autres qui se les approprient et les remettent dans d'autres sites sur le net ...
On finit par trouver une multitude de sites donnant de mauvaises données (mais les mêmes) et c'est bien difficile de se rendre compte qu'elles sont issues toutes d'une même connerie initiale.
C'est le problème du net.
C'est un merveilleux outil d'information, mais comme n'importe qui peut y écrire n'importe quoi, c'est difficile de faire la part des choses.
Sur cela près, on ne pourra pas refaire le monde.

Alors là je ne sais pas quoi dire, si ce n'est un grand merci...
Je suis vraiment désolé, je ne m'étais pas douté de ces erreurs (je veux dire les miennes et celles de l'énoncé) ... Mais maintenant j'y vois plus clair ! Merci énormément, désolé de vous avoir fait perdre du temps là-dessus...
Mais merci beaucoup !!


