Inscription / Connexion Nouveau Sujet
le laser
Le laser est considéré comme une source de lumière monochromatiqe avec un faisceua de lumière qui peut être considéré comme " non divergente" dans une certaine limite...
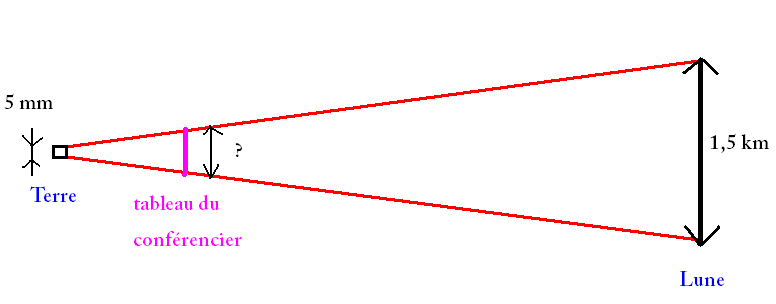
La divergence d'un faisceau laser est telle qu'un faisceau de 5mm de diamètre sur Terre,pointé vers le ciel,possède un diamètre de 1,5km sur la lune(qui est à 3,84*105km).En déduire le diamètre d'impact du faisceau d'un tel laser qui servirait de pointeur à un conférencier lorsque celui-ci éclaire u tableau placé à 20m.
est ce que vous pourriez m'expliquer ce qu'il faut faire ou même me donner des piste s'il vous plaît. Je vous remercie d'avance.
Bonjour,je l'ai compris donc si j'ai bien interpreté je dois chercher le diamètre?
donc, je fais 1,5 km nous fais 1500000 mm
1500000-5,5 ce qui me fais 1499994,5 mm
c'est tout?
C'est censé être le diamètre de la tache sur le tableau du conférencier ta valeur de 1499994,5 mm ??
Bonjour,
Etant donné que tu n'as pas eu de réponse de athrun depuis hier, j'interviens simplement pour te réfléchir un peu sur ton résultat.
Le conférencier est à 20m d'un tableau qu'il éclaire avec son laser, et d'après toi, le faisceau qui faisait à la base 5 mm de diamètre fait maintenant une tache sur le tableau de 1 499,9945 m, soit une tache de 1,5 km, la même chose que sur la lune alors que le tableau n'est situé qu'à 20m du conférencier et que la lune est à plus de 300 000km.
C'est important de vérifier ses résultats en cherchant le sens physique de ce que l'on a trouvé et pas simplement lâcher un résultat numérique comme ça...
Si tu n'as pas encore trouvé la réponse, essaies voir de faire un tour dans tes "vieux" cours de mathématiques du collège, tu trouveras sûrement le théorème à utiliser...
Bonsoir bibe 
merci pour cette explication qui était exactement celle qu'il fallait donner.
lyndsey tu comprends ainsi que le résultat trouvé est aberrant (d'ailleurs je me demande quelle méthode tu as utilisé pour y parvenir).
Si tu n'as pas encore trouvé la réponse, essaies voir de faire un tour dans tes "vieux" cours de mathématiques du collège, tu trouveras sûrement le théorème à utiliser...
en effet, la figure parle d'elle-même aussi.
Boujour, j'ai beau chercher mais je ne sais quoi faire.De plus la figure ne me pare absoluement pas.
J'ai placé les points A,B,C,D,E sur la figure.
On connaît :
OF = 2,5 mm
OB = 20 m
OC = 3,84.105 km
CD = 0,75 km
On cherche BE.
Commençons par déterminer AO :
Comme ça on aura .
On a
peux-tu trouver AO avec ceci ?
DONC, BE= (OF*AB)/AO on sait que AB= AO + OB
[2.5*10-6*X*(3.333333333*10-6X +2.0*10-5 )] /3.333333333*10-6