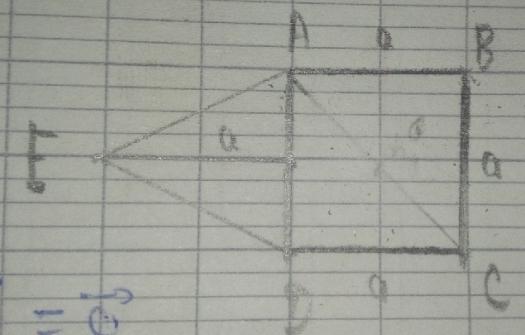
Je sais que G1 et barycentre du triangle AED mais comment trouver sa position ? Et G2 barycentre ABCD.
Si on trace le diagonale on aura deux triangle rectangle ,bah moi je prends ADC  => d'après la propriété de Pythagore on a:
AC²=AD²+DC²=a²+a²
=9+9=18 =>AC=3√2 =>AG=3√2/2

Remarque préliminaire concernant l'énoncé :
On ne voit pas trop comment BD, diagonale du carré dont les côtés ont une mesure de 3cm peut avoir la même mesure de 3cm

Le centre de gravité d'un triangle se trouve au point de concours des médianes.
Ce point de concours que tu appelles G₁ se trouve au 2/3 de chaque médiane en partant du sommet.

Le calcul de AG n'a guère d'intérêt.
Il est clair, que le centre de gravité G du carré se situe au point de concours des diagonales.

Une fois les positions de G et de G₁ connues on calcule la distance GG₁
On concentre la masse m du carré en G et la masse m/2 du triangle en G₁

Le centre de gravité de la plaque est aussi le centre de gravité des points G et G₁ affectés des masses m et m/2

OK mais s'ils vous plaît comment vous avez fais pour savoir que le point de concours se trouve au 2/3 du  médian?

La position de G1 c'est 2/3 du médiane .

Je l'ai appris à l'école voilà pas mal d'années.

Ah OK merci .  Donc j'aurai sois G barycentre de G1 et G2 =>
mGG1+m/2GG2=0(vec nul)

Si G₁ est le barycentre du triangle et G₂ celui du carré (de masse double) tu auras :



ou bien en multipliant par 2 les deux membres de cette égalité :

OK ! Voilà j'ai trouvé :
G1G=2/3G1G2

Exact !
Reste à trouver la valeur de la longueur G₁G₂

Je croyais que c'est fini.
Là vraiment je n'ai aucune idée ,un coup de main s'ils vous plaît

G₂ est au centre du carré.
G₁ aux 2/3 de la médiane du triangle en partant du sommet, donc au tiers en partant de la base.
Donc G₁G₂ = ...... cm

Eh bien comme G2 centre du carré =>AG2=3√2/2 AC
Pour tout vous dire jusqu'à présent je ne sais pas comment m'y prendre .

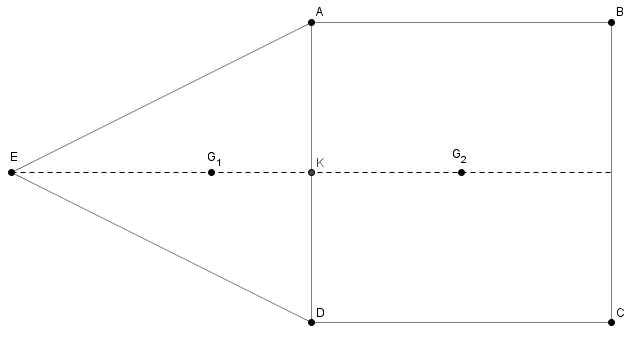
Soit G le centre d'inertie de la plaque.

L'énoncé indique que :
AB = BC = CD = DA = EK = a = 3cm

Les règles de géométrie concernant le triangle et le carré indiquent que :
EG₁ = (2/3) EK  et  KG₂ = a/2

Tu as trouvé que :
GG₁ = (2/3) GG₂

L'énoncé demande de (je cite) :
" Déterminer la position du centre d'inertie de cette plaque. "
ce qui revient à calculer soit G₂G, soit KG, soit GG₁

Voilà j'ai trouvé :
KG=1/2KG₂= 1/2×3/2=3/4=0,75cm

Comment as-tu fait pour trouver  KG = 1/2 KG2 ?

Même si cela était exact, cela n'aurait aucune valeur puisque non démontré.
Mais c'est faux.

Pourquoi ne pas suivre mes conseils ( Voir mon post du 28-12-18 à 20:52 )
a) Tu calcules G₁G₂
b) tu te sers de ton résultat : GG₁ = (2/3) G₁G₂

Attention : Dans mon post du 29-12-18 à 16:27 j'ai écrit:
Tu as trouvé que :
GG₁ = (2/3) GG₂
alors qu'il fallait écrire :
GG₁ = (2/3) G₁G₂

Merci pour votre patience.
Bon je propose :
G₁G₂=3/2GG₁

OK!
G₁k+KG₂=1+1,5=2,5cm

Nous sommes d'accord !

Tu avais trouvé (28-12-18 à 20:42) : G₁G=2/3G₁G₂ :
Tu viens de trouver : G₁G₂ = 2,5 cm

Tu peux donc maintenant calculer la valeur de G₁G et positionner correctement G c'est à dire
" Déterminer la position du centre d'inertie de cette plaque. "
comme c'est demandé par l'énoncé.

Je remplace seulement G1G2 par sa valeur :
G1G=2/3×2,5=1,6cm

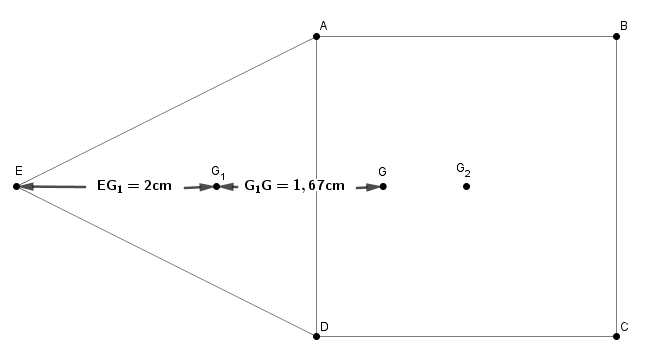
Je préfère G₁G = 1,67cm
ou bien si on préfère repérer la position de G par rapport à celle de E :
EG = EG₁ + G₁G = 2,0 + 1,67 = 3,67cm

OK OK je comprends mais j'ai vu dans certain correction des exos de ce chapitre :
Il se limite seulement à cet genre d'écriture G1G=2/3G2G1 sans déterminé l'autre distance en cm .
Est-ce une erreur ?

Tout dépend de la question posée.
Ici, elle est très claire : " Déterminer la position du centre d'inertie de cette plaque "

G1G=2/3G2G1 ne répond pas à cette exigence et n'est donc pas la réponse attendue.

Ah OK je comprends .
Vraiment je vous remerci beaucoup de m'avoir pris de ton temps pour m'aider .Merciii😊