Inscription / Connexion Nouveau Sujet
La vitesse d'une masse
Bonjour
J'aurais besoin d'aide pour cet exercice :
Chapitre : énergie cinétique.
Une masse m supposée ponctuelle est fixée à l'exterimite d'un fil AB de longueur l=1 m.
Le pendule ainsi constitué est écarté de sa position d'équilibre d'un angle 
,le fil restant tendu.
On lance alors la masse m vers le bas avec une vitesse V0.
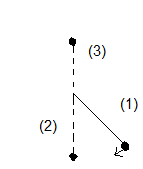
Le vecteur vitesse 0 étant perpendiculaire au fil (voir croquis)
a) Calculer la vitesse de la masse m au moment où le fil fait avec la verticale
-Un angle de 30°
-Un angle de 0°
On donne V0= 2 m/s; =60°
b) Le fil peut-il remonter jusqu'à la verticale (position 3 )? Si oui, quelle est alors la vitesse de la masse m au moment où le fil passe cette position ?
Mes réponses :
a)
Système: la masse
BFA: P, T
TEC: Ecf-Eci=
W (Fext)
Ecf=0 car sa vitesse est nulle et W (T)=0 ? <==>
-1/2 mV^2= mgh or h= l-lcos(30°) alors
V= 1,64 m/s ?
Merci d'avance
Salut beugg, c'est encore moi !
Votre méthode d'approche du problème est correcte, mais certaines choses sont à revoir.
En considérant que :
*l'état initial est la position où i = 60° et vi = V0 = 2 m.s-1 ; l'énergie cinétique initiale n'est donc PAS nulle ; on a : Ec = 1/2 m vi2
*l'état final est la position où f = 30° (ou 0°), vf étant la vitesse à calculer ; l'énergie cinétique finale, n'est pas nulle elle non plus ; on a : Ec f = 1/2 m vf2
Pour le calcul du travail du poids, l'expression de la hauteur h à prendre en compte est elle aussi à revoir.
Pour justifier que le travail de la tension est bien nul, vous pouvez dire, par exemple que la puissance instantanée de la tension, puisque les vecteurs
et
sont perpendiculaires.
N'hésitez surtout pas à faire plusieurs schémas illustrant chacun la situation envisagée :
1° schéma i = 60° et f = 30°
2° schéma i = 60° et f = 0°
On regarde la question b) ensuite.
P.S. Si vous en avez assez de voir que c'est souvent moi qui vous répond, n'hésitez pas à me le dire, je m'abstiendrai pendant quelques jours et je ne me vexerai pas pour autant.
A plus (si vous le souhaitez !).
Salut Picard
OUI pour votre conseil, on hésite pas.
Je suis très content de vous.
L'île de la physique-chimie toujours la meilleure!
Ok
suivant les indications qui sont très clairs, on a:
V2f= 2gh+V2i
or h= l-lcos (60°) <==>
Vf= 3,46m/s ?
D'accord pour : vf2 = vi2 + 2 g l (1 - cos 60)
lors du passage du pendule par la position d'équilibre (f = 0°) mais la valeur numérique est à revoir.
Il faudra aussi calculer la vitesse lorsque f = 30°
2° schéma
alpha initial = 60°
alpha final= 0°( donc la vitesse sera nulle)
<==>
-1/2.mVi^2= mgl
Vi2= -2gl
Est-il juste ?
alpha final= 0°(
Non, ça n'a pas de rapport, c'est même dans cette position que la vitesse sera maximale.
Ce qui est nul, à cet instant, c'est la puissance instantanée du poids
Vitesse au passage par la position d'équilibre :
f = 0°Etat initial : vi = V0 = 2 m.s-1
i = 60°Etat final : vf à déterminer
f = 0°On tire :
A.N. vf2 = 22 + 2
101 (1 - cos 60°) Soit, finalement : vf = 3.74 m.s-1
Vitesse au passage par la position intermédiaire (cf schéma) :
f = 30°Etat initial : vi = V0 = 2 m.s-1
i = 60°Etat final : vf à déterminer
f = 30°On tire :
A.N. vf2 = 22 + 2
101 (cos 30° - cos 60°) Soit, finalement : vf = 3.36 m.s-1
***Image recadrée***
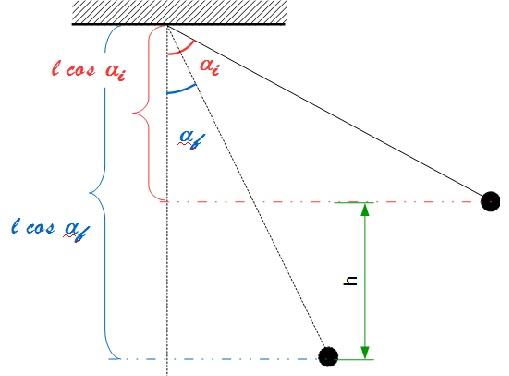
Regardez le schéma !
La hauteur h dont descend le pendule est la différence entre l cos f et l cos i
La dernière ligne est correcte, mais je ne comprends pas trop les deux premières.
Pour la question b) je vous répondrai demain, pour le moment, je dois me déconnecter.
Donc h= 2l ?
Voici quelques pistes pour traiter la question b).
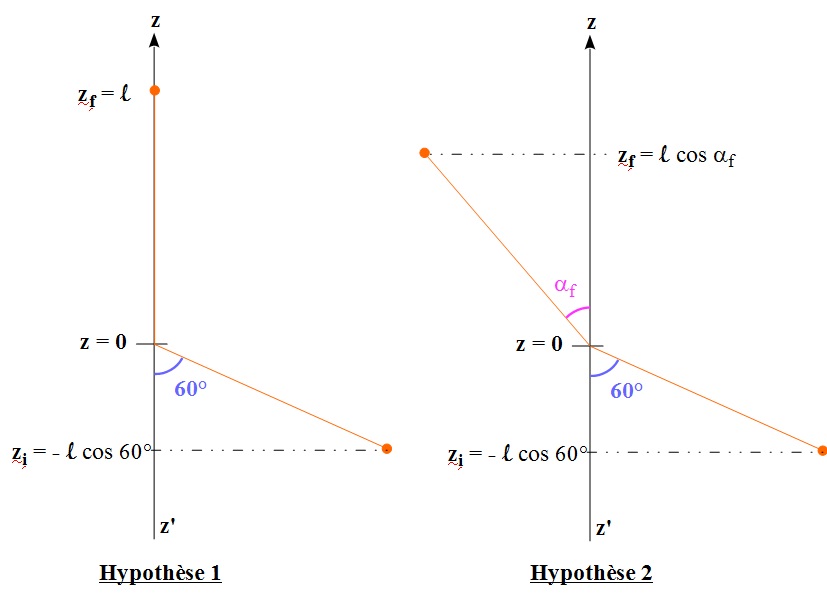
Faire un schéma envisageant les deux hypothèses (cf image jointe).
Choisir un axe des altitudes z'z, orienté positivement vers le haut et d'origine z = 0 au point d'attache du fil du pendule.
Exprimer le travail du poids non pas sous la forme mgh, mais sous la forme
Appliquer le théorème de l'énergie cinétique entre l'instant initial où
i = 60° et l'instant final correspondant à l'hypothèse envisagée.
Pour l'hypothèse 1, déterminer l'expression de Ecf ou celle de vf2 et conclure.
Pour l'hypothèse 2, déterminer l'expression de
f sachant que vf = 0, enfin calculer f.
P.S. Un conseil très général, l'expression du travail sous la forme
travail de la force électrique :
travail de la force élastique :
Je viens de relire l'énoncé et de constater qu'on ne demande pas la hauteur maximale à laquelle le pendule peut remonter ; la seconde hypothèse que j'ai envisagée n'a donc pas à être traitée.
Dommage...
Ok
Donc cela veut dire que:
Le fil ne peux pas remonter jusqu'à la position (3) car sa vitesse est faible ?
Effectivement, le pendule ne remonte pas jusqu'à la position 3, mais de quelle vitesse parlez-vous ?
Je me demande si vous avez bien compris ce qui se passait.
Le pendule est lancé depuis la droite avec une vitesse initiale. Il passe sur la partie gauche mais ne peut pas aller jusqu'à la verticale. Il ralentit et rebrousse chemin quand sa vitesse s'annule.
OK ?
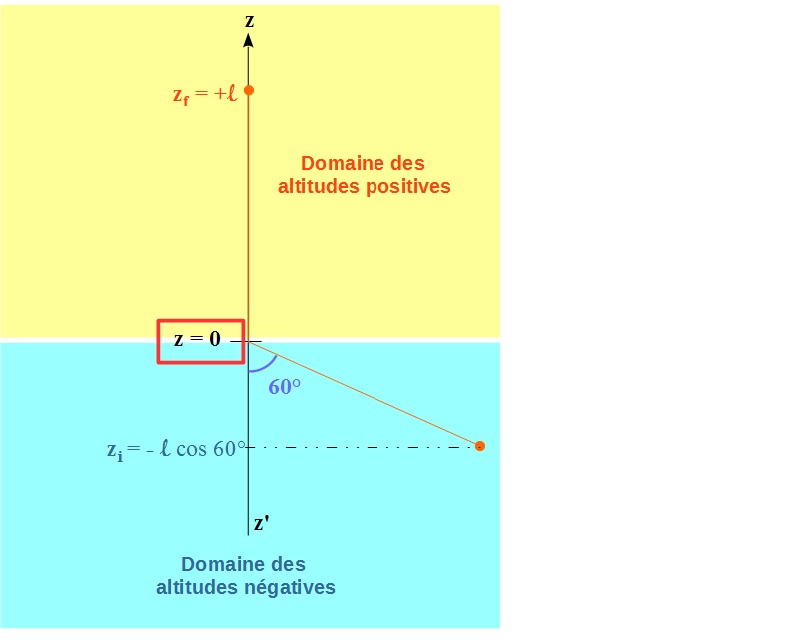
J'ai choisi comme origine des altitudes, le point d'attache du fil du pendule au support fixe, l'axe des altitudes étant évidemment vertical et orienté positivement vers le haut.
Dans ces conditions...
*tous les points situés au dessus du point d'attache ont une altitude positive 
zf = + l
*tous les points situés au dessous du point d'attache ont une altitude négative zi = - l cos 60°
Oui c'est très clair
C'est moi qui absente parfois
Merci merci 1000 fois pour votre aide précieuse
Donc au revoir
À très bientôt
Bonne journée
Annuler
connectez vous