Bonsoir Pitchoune,

en effet l'enonce ne donne pas la profondeur du puits. mais on n'en a pas besoin jusque la question 5, a laquelle on demande de la calculer pour pouvoir traiter la derniere question. Donc... tu aurais du faire les 4 premeires question sans etre bloquee ! (ou alors il y a autre chose qui te bloque).

1 - C'est une relation de cours, mais il faut que tu revoies le mouvement d'un objet soumis a l'acceleration de la pesanteur g.
Il faut aussi choisir un axe vertical (puisqu'ici la pierre tombe verticalement). Prends l'habitude de faire ce que je fais : on oriente l'axe verical OZ de bas en haut, et on prend son origine O au niveau de la surface du sol (ce serait bien que tu fasses la figure en meme temps...). Il  a des petites inconvenients : l'acceleration de la pesanteur, dirigee vers le centre de la Terre, se projette negativement sur cet axe et s'ecrit donc comme -g ; la vitesse aussi a une projection negative, puisque la pierre tombe (donc elle se dirige vers les z negatifs). Et la position z de la pierre aussi, puisque elle quitte le sol a la valeur z = 0 et  tombe ensuiet dans le puits... Ces signes - ne sont pas genants car, en fin de compte, ils permettent de verifier que la solution trouvee est bien correcte.
Bon, v est la vitesse, elle se mesure en m.s^-1. Le temps t se mesure, lui en secondes. L'acceleration de la pesanteur, g, vaut 9,80 m.s^-2.Ce qui veut dire qu'avec ce choix d'unites on trouve toutes les distances en m et les vitesses en m/s.
Moyennement quoi, la relation liant v a t s'ecrit v(t) = -gt. Avec g = + 9,8 m.s^-2.

2 - A t = 1 s, cette vitesse vaut - 9,8 m/s. Le signe - indique bien que la pierre se dirige vers le centre de la Terre.
A t =  2 s, on arrive a v = - 19,6 m/s.

3 - maladresse dans l'ecriture de ton enonce. Je suppose qu'au lieu de "rectiligne et uniforme " il faut lire "rectiligne uniformement varie". La bonne reponse est alors celle-la, puisque la pierre tombe en restant sur l'axe OZ (donc elle possede un mouvement rectiligne), mais que sa vitesse augmente avec t suivant une fonction lineaire (-gt), donc mouvement rectiligne uniformement accelere.

4 - Voir ton cours, car si je connais la reponse je ne peux pas savoir comment ton professeur te l'a explique. La reponse est z = -(1/2)g.t². Donc z(t) est bien proportionnel a t².

5 - Du coup, si la duree de la chute est t1 = 1,6 s, on trouve sans probleme z = -12,5 m. Le signe negatif indique que la pierre s'est dirigee vers les z negatifs (ca fait un moment qu'on le sait...). La profondeur du puits est donc h = 12,5 m.

Je laisse volontairement la derniere question de cote, car si tu as compris tout ce que je viens de te dire, tu devrais facilement en trouver la reponse. Sinon ets uj post, et je continuerai a expliquer.  Prbebo.

Merci pour ta réponses sa m'aide un peut mais je ne comprend pas tout.

A l'exemple l'histoire des moins "-" pour dire qu'on va vers la terre je ne l'ai pas vu en cours.

Aussi je ne comprend pas comment tu arrive a trouver le nombre de mettre parcourue a la 5)

Enfin a la 6 je ne vois toujours pas comment trouver sans avoir la hauteur que la pierre chute :s

OK pitchoune, je vois ce qui te bloque.
Imagine un mobile qui se deplace sur un axe OX, qui se trouve en x = 0 a l'instant initial et qui ensuiet se dirige vers les x decroissants : sont abscisse x(t) est alors constamment negative, es-tu d'accord ? Du coup il y a deux facons de l'ecrire : ou bien on pose x(t) = A.t, et dans ce cas A est negatif (ici j'ai suppose que le mouvenent du mobile conduisait a une loi x(t) lineaire), ou bien on ecrit x(t) = -At, et dans ce cas A est positif.
C'est la meme chose, est-ce que tu comprends ca ?
Si tu veux, demain on reprendra l'explication mais en orientant l'axe des z vers le bas. Il n'y aura plus de signe negatif, mais en copmparant les deux corriges tu devrais t'apercevoir qu'ils sont equivalents et fournissent les memes reponses. Je ne fais pas ca maintenant, car il est 22 h et demain je me leve tot...

Pour ta remarque concernant la question 6, je te rappelle que si on a repondu correctement a la question 5 il n'y a plus aucune difficulte pour terminer l'exercice.

A demain,  BB.

Bonsoir Pitchoune,

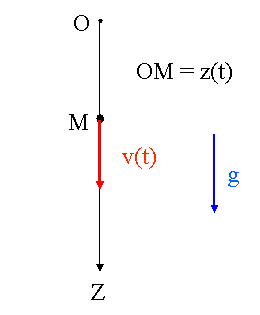
alors on reprend ma solution precedente, mais en orientant cette fois l'axe vertical vers le bas, et en prenant son origine O au niveau du puits. Regarde le schema ci-dessous, ou j'ai represente en bleu l'acceletation de la pesanteur, en rouge la vitesse de M a un endroit quelconque dans le puits. Maintenant, toutes les flexhes sont dans le meme sens.

1 - Relation du cours : v(t) = gt, avec g = 9,8 m.s^-2. On a pris l'instant initial (t = 0) au moment ou on lache la pierre, donc en cet instant elle n'a pas encore de vitesse.

2 - A t = 1 s, on trouve v = 9,8 m.s^-1, a t = 2 s on trouve 19,6 m.s^-1, et ainsi de suite.

3 - c'est un mouvement rectiligne, puisque le mouvement de M se passe sur l'axe OZ, mais il est rectiligne uniformement accelere (ca veut dire que la vitesse augmente avec le temps selon une fonction affine, qui est ici une fonction lineaire. Ca, tu dois savoir ce que c'est).

4 - Il doit y avoir dans ton cours une relation qui decrit completement le mouvement rectiligne uniformement varie : je te la donne, c'est z(t) = (1/2).gt² + V₀t + z₀. Si tu ne l'as pas ce n'est pas grave, car on ne va garder que le premier terme : en effet, z₀ est la position de M en t = 0, et comme c'est la qu'on a place le point O z₀ et nul ici ; de meme V₀ represente la vitesse quand t = 0, et comme a cet instant on laisse tomber la pierre sans la lancer, V₀ est nulle elle aussi.
On a donc : z(t) = (1/2).gt².

5 - Cette relation permet de calculer la distance z parcourue par la pierre a partir du sommet du puits : par exemple pour z = 0,2 s on trouve z = 0.196 m ; pour t = 0,6 s, z = 1,76 m. Et ainsi de suite.
Maintenant relis bien l'enonce de la question 5, car c'est la que tu butes :
On te dit que la pierre atteint le fond du puits au tems t = 1,6 s (la hauteur de chute, c'est ca !). Donc la relation ci-dessus fournit z(pour t = 1,6) = 12,5 m. La profondeur du puits est donc h = 12,5 m.

6 - Pour faire cette derniere question tu n'as pas besoin de connaitre h : il suffit d'avoir compris que la pierre atteint le fond du puits al'instant t = 1,6 s. Avec la relation v(t) = gt, on obtyient facilement v(pour t = 1,6) = 9,8 x 1,6 = 15,7 m.s^-1.

Est-ce que ce dorrige te convient mieux ? Je peux difficilement etre plus clair, il faut que toi aussi tu fasses un effort de comprehension.

A bientot,  BB.

J'ai enfin compris l'explication en général mais le souci est que pour la 5) je but encore. Car je ne vois pas par quoi il faut multiplier le temps pour trouver la hauteur

Pitchoune, je suis oblige de repeter que je ne peux pas etre plus clair !
La question 5 est " Quelle est la hauteur (h donc) de la chute si la durée (de cette chute donc) est de 1,6 s ?".

Si tu as compris la relation trouvee en 4, cad z = (1/2).g.t², qui donne la distance z parcourue a chaque instant t, il suffit de reporter dans cette relation le temps t = 1,6 s de la chute pour  savoir quelle distance z la pierre a parcourue. Et cette distance, c'est forcement la profondeur h du puits, puisque ensuite la pierre ne tombe plus !!   BB.