Inscription / Connexion Nouveau Sujet
l'energie mecanique
bonjour tt le monde
j'arrive pas resoudre ce probleme la ca sera aimable de votre part de m'aider
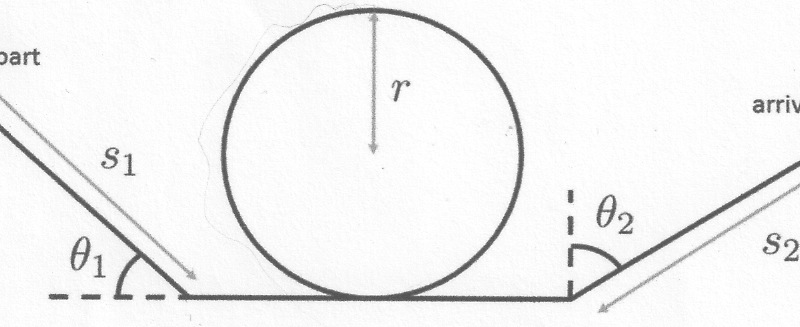
des rails forment un plan incliné suivi d'une boucle circulaire de rayon r suivie d'un autre plan incliné
1) si le train glisse sans frottement sur les rails et qu'il part de repos au point de départ quelles conditions doivent etre verifier pour que le train puisse franchir la boucle pour se rendre au point d'arrivée
2)en choisissant le bas de la boucle comme le point de reference pour l'energie potentielle gravitationnelle detreminer en fonction de m.r.g teta entre l'horizentale et le premier plan incliné et enfin S1 la longuer du premier plan incliné l'energie cinematique minimal que doit avoir le train au depart pour rester en contact avec la piste sur la boucle
3) on donne teta:45 S1:2m r=1m la masse du train miniature est 0.5kg donner la valeur numerique de l'energie cinetique minimale obtenue en question 2
Bonjour,
Pour que le train passe le point haut de la boucle en restant en contact avec les rails (une réaction de contact nulle n'étant acceptable qu'en ce seul point haut) et en conservant son mouvement circulaire il faut que sa vitesse en ce point soit suffisante.
Tu dois faire le bilan des forces appliquées au train et écrire le principe fondamental de la dynamique (ou deuxième loi de Newton) pour ce point haut de la boucle, connaissant l'accélération qui correspond au mouvement circulaire du train (toujours en ce point).
Note : ton énoncé n'est pas d'une grande clarté.
Je crois comprendre que pour la première question le départ se fait à vitesse nulle ("au repos") mais que pour la deuxième question, il faudra chercher une vitesse minimale au départ. Est-ce cela ?
D'autre part, y a-t-il un schéma avec cet énoncé ? Comment se font les passages des plans inclinés à la boucle ?

wii effectivement il faut trouver la vitesse d'abord dans la deuxiéme question en fait je sais pas comment vous montrer le shéma de cet enoncé
mais juste je veux savoir ca veut dire koi le point de reference de l'energie potentielle gravitationnelle
je vais essayer de vous montrer le shéma pour le premierplan incliné le train descend avec un angle teta 1 avec l'horizental puis il passe par la boucle (looping) et finalement le train monte dans le deuxiéme plan inchliné
voila j'espére ke j'ai pas expliquer
et merci d'avance
1.
Selon moi, le schema se divise en deux etapes:
1er etape:
Puisque la balle part du repos, Vo= 0m/s, Ki=1/2mVo^2=0.
Nous sommme sur un plan incliné, dong la valeur de Ugi = mgDsin0.
Ceux-la correspond l'energie initial. Donc, Ei=mgDsin0
Nous allons prendre le point le plus haut du cercle comme position finale. Donc, nous avons Ef= kf+Ugf= 1/2vf^2+mg2r
Ei=Ef ==> mgDsin0 = 1/2vf^2 + mg2r
Tu isoles le Vf afin d'obtenir son equation qui te permettra de trouver sa valeur.
A la deuxieme étape, tu refais la meme chose, sauf que cette fois-ci, Ei est égale au ki+Ui du point le plus haut du cercle. Et le Ef du point d'arrivé.
Mais voila: d'abord, j'ignore si ma demarche est pertinent et juste. De plus, elle ne repond pas a la question puique il nous demande les CONDITIONS pour arriver au point d'arriver.
Comment dois-je interpreter ces équations? Devrais-je introduire la dynamique au point le plus haut du cercle? Donc, Fy= N-mg=mv^2/2 ===> N=0, afin de répondre a la question? Au bien, je n'emploie pas le bon raisonnement, ni les bonnes equations?
J'aimerais bien avoir un reponse.
JE NE VEUX PAS UN REPONSE! CA NE SERT A RIEN! Je veux une explication. Merci
Bonjour fmtristan
Merci d'avoir posté le schéma de l'exercice.
Bonjour Poplolita
Tu cherches dans les bonnes directions.
Ta première idée a été de vérifier que le train (ce n'est pas une balle) a au départ assez d'énergie pour atteindre le haut de la boucle.
Mais ce n'est peut-être pas la condition la plus exigeante.
Que se passe-t-il si le train a juste assez d'énergie pour atteindre le haut de la boucle ? Il y arrive à vitesse nulle et donc : il tombe !
Il faut en conséquence que tu creuses ta seconde idée : il doit avoir assez d'énergie non seulement pour atteindre le haut de la boucle mais il doit avoir en ce point une vitesse suffisante pour ne pas tomber, c'est-à-dire pour rester en contact avec les rails ; traduction pour un physicien : la vitesse doit être telle en ce point que la réaction des rails existe, ou, à l'extrême rigueur, s'annule tout à fait ponctuellement.
Il faut donc trouver la condition qui permet, au sommet de la boucle, d'avoir
Note : petite difficulté avec le Canada : à 4 heure du matin, heure en France, je dors !