Inscription / Connexion Nouveau Sujet
L'arc à l'armature qui se deforme. (E, Ec, Ep)
j'espère que vous allez bien !!
j'étais bloqué sur un exercice de physique, un chapitre sur les énergies (mecanique, potentielle & cinétique)
je vous laisse l'énoncé
 :
:
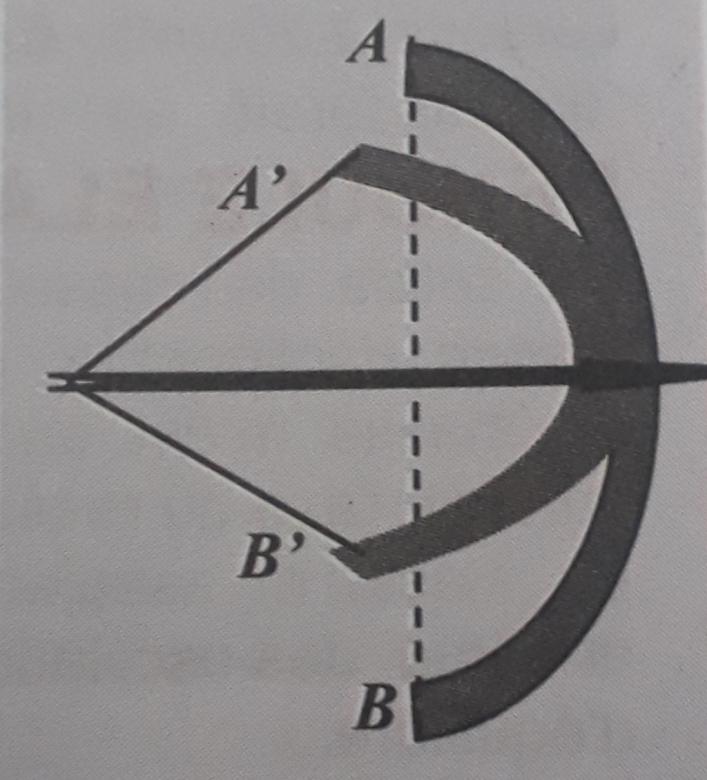
On dispose d'un arc
(voir croquis)
- l'arc n'est pas tendu : on donce AB = 110 cm
- l'arc est tendu par l'archer : A'B' = 80 cm
La corde est inélastique, l'armature seule se deforme. La flèche est placée au milieu de la corde.
1-) A l'équilibre la force exercée par l'archer est horizontale d'intensité F = 160N.
2-) La flèche est tirée verticalement vers le haut. Elle parcourt 30 m avant de redescendre.
- calculer sa vitesse initiale.
- calculer le travail minimal fourni par l'archer pour tendre la corde.
merci d'avance ![quote]
Bonjour,
Je n'ai vu ni le croquis annoncé, ni l'exposé de ce que tu as essayé de faire avant de poster ton message.
Aurais je mal cherché ?
à vrai dire je ne sais pas comment joindre un croquis ? je suis "nouvelle" sur le forum !
moi aussi, c'est surtout la première question qui me pose problème...
j'ai pensé à passer par le travail, ou peut - être dire que la force est la même ? mais ça semble beaucoup simple...
Le croquis fait partie de l'énoncé. Ne pas le joindre revient à donner un énoncé incomplet.
Etre un nouvel utilisateur du forum ne dispense pas d'apprendre à s'en servir !
Pour insérer une image voir la FAQ et plus particulièrement ici ![]() [lien] la Q05
[lien] la Q05
Ton alinéa noté "1) " ne comporte aucune question !
Pense à vérifier ce que tu as posté et à le comparer avec l'énoncé original.
Car comment répondre à une question qu'on ne connaît pas ?
je me suis trompée, j'ai mal recopié la première question de l'énoncé !
elle est complétée par :
"calculer la tension de chaqur brin de la corde"
je m'excuse pour ce manque de rigueur 
** image supprimée **
Voici quelques éléments pour t'aider à démarrer :
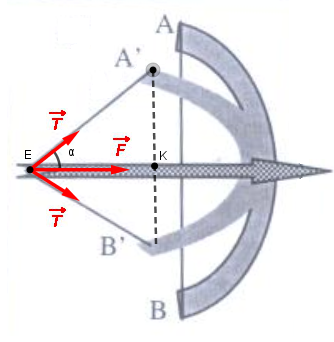
La corde étant inélastique tu as : A'E = B'E = AB/2
et
sin ( )=A'K / A'E
)=A'K / A'E
A partir des valeurs de  et de F on obtient celle de T
et de F on obtient celle de T
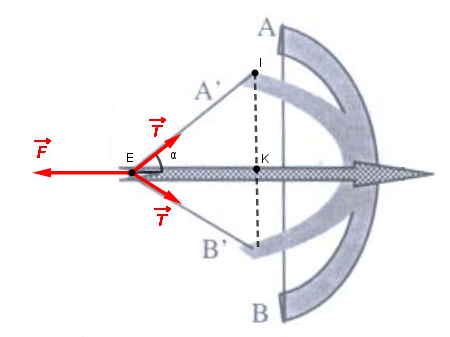
Désolé.
La force étant exercée par l'archer était évidemment mal orientée.
Ci dessous la figure corrigée.
Cela ne change rien pour les indications que j'ai données.
bonsoir,
est - ce que je peux considérer une composante de T ; Tx ? en me disant que Tx = -(-F ) = F
puis que
Tx = Tcos(a)
T= Tx / cos(a)
d'où
T = F / cos(a)
Tu y es presque :
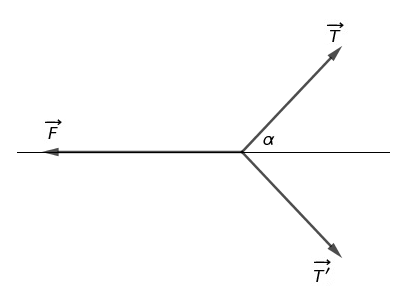
A l'équilibre la somme des forces qui s'exercent est nulle :
On projette cette relation sur l'axe un axe Ox horizontal orienté vers la droite :
T cos(α) + T' cos (α) - F = 0
Or T = T' pour des raisons de symétrie.
Donc F = 2T cos(α)
et T = F/(2 cos(α)