Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Images données par 2 lentilles

Posté par
fanfan56 29-12-14 à 10:10

Bonjour ,

Exercice 4
4-1 Une lentille mince convergente L1 a une distance focale f'=30 cm. Un objet réel est placé à 1 m de la lentille, calculer la distance entre l'image et le centre optique de la lentille.
Faire une construction.

4-2 On place une lentille divergente L2 de distance focale f' = -10 cm à une distance de L1 telle que O1O2= 30 cm  ( je ne sais pas comment mettre le trait sur O1O2)

Que représente l'image donnée par L1 pour L2?
Calculer la position de l'image finale donnée par L2.
Faire une construction.


Voici pour le 4-1

4-1 Une lentille mince convergente L1 a une distance focale f'=30 cm. Un objet réel est placé à 1 m de la lentille, calculer la distance entre l'image et le centre optique de la lentille.
Faire une construction.

La relation s'écrit:
1/(OA') - 1/(OA) = 1/(OF') = 1/f'  avec OA distance objet-lentille; OA' distance image-lentille et OF'= f' distance focale

on connaît OA = -1m et f' = 30 cm soit: 0,30 m

On cherche OA', on écrit 1/(OA') = 1/(OF')-1/(A)  soit: 1/(OA') = 1/0,3-1/1,0
Ce qui donne: 1/(OA') = 1/0,3 -0,3/0,3 = 2,33

OA' = 1/2,33 = 0,4291 soit 0,43

OA' = 0,43 m
                                                                                                                    

Posté par
Coll Moderateurre : Images données par 2 lentilles 29-12-14 à 10:48

Re - bonjour,

Oui, c'est cela, mais il ne faut pas tronquer les résultats intermédiaires. Seul le résultat final peut (et doit) être arrondi.

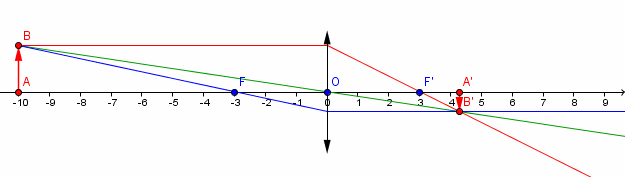
Images données par 2 lentilles

L'unité de mesure sur mon graphique est le décimètre

Pour écrire les mesures algébriques... il faut passer par le \LaTeX ! Une habitude à prendre (mais un petit investissement au début).

Relation de conjugaison pour une lentille mince de centre O, relation dite de Descartes
Le pied de l'objet est en A
Le pied de l'image est en A'
Le foyer image est en F'
L'axe optique est orienté (dans le sens de propagation de la lumière)

\large \frac{1}{\ \bar{OA'}\ }\;-\;\frac{1}{\ \bar{OA}\ }\;=\;\frac{1}{\ \bar{OF'}\ }

Or ici :
\bar{OA}\,=\,-\,1,0 \,\rm{m}
et
\bar{OF'}\,=\,0,30 \,\rm{m}

On en déduit immédiatement que :

\large \bar{OA'}\;=\;\frac{\ \bar{OF'}\ \times\ \bar{OA}\ }{\ \bar{OF'}\ +\ \bar{OA}\ }

Application numérique :

\large \bar{OA'}\;=\;\frac{\ 0,30\ \times\ (-1,0)\ }{\ 0,30\ +\ (-1,0)\ }\;\approx\;0,428\, 571\,...\;\rm{m}

Tu vois que ce n'est pas tout à fait le même résultat que le tien et cela parce que tu as tronqué un résultat intermédiaire, ce qu'il ne faut pas faire.

Évidemment il faut arrondir et je suis d'accord avec ton résultat de 0,43 m ou 43 centimètres

Posté par
Coll Moderateurre : Images données par 2 lentilles 29-12-14 à 10:51

Et pour écrire une mesure algébrique : par exemple \bar{OA}
. tu tapes \bar{OA}
. tu sélectionnes cela
. tu cliques sur le petit bouton LTX qui se trouve en bas du cadre d'écriture au-dessus de "Aperçu"
. cela place des balises [tex][/tex] autour de la sélection
. comme ceci : [tex]\bar{OA}[/tex]

N'oublie pas de vérifier avec "Aperçu" avant de poster !

Posté par
fanfan56re : Images données par 2 lentilles 29-12-14 à 18:11

4-2 On place une lentille divergente L2 de distance focale f' = -10 cm à une distance de L1 telle que O1O2= 30 cm  ( je ne sais pas comment mettre le trait sur O1O2)

Pour cette partie de l'exercice, j'ai fait un schéma.

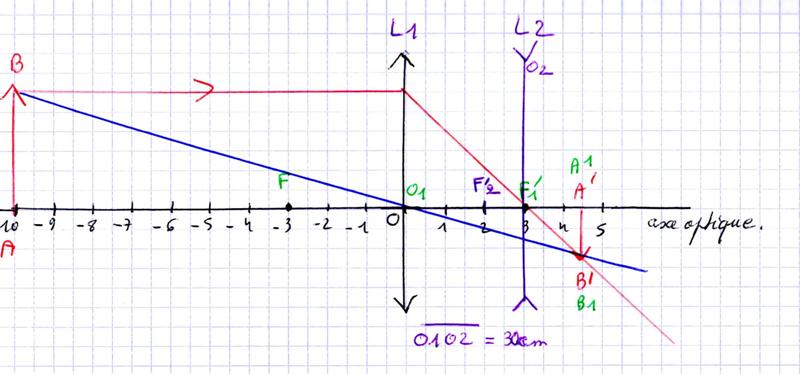
Images données par 2 lentilles

Posté par
fanfan56re : Images données par 2 lentilles 29-12-14 à 18:12

Après, je ne vois pas trop quoi faire??

Posté par
Coll Moderateurre : Images données par 2 lentilles 29-12-14 à 18:39

Ça progresse bien !

Bien sûr l'image A1B1 donnée par la lentille convergente L1 n'existe plus dès que la lentille divergente L2 est interposée dans les rayons qui formaient cette image.

1)

Citation :
Que représente l'image donnée par L1 pour L2 ?

Pour la lentille convergente L1 : A1B1 est une image réelle
Pour la lentille divergente L2 : A1B1 est...

2)
Citation :
Calculer la position de l'image finale donnée par L2.

Pas de difficulté particulière :
. Tu connais la relation de conjugaison
. Tu connais également les valeurs de \bar{O_2A_1} et de \bar{O_2F'_2}

3)
Citation :
Faire une construction.

Ton rayon rouge passe par le centre optique de la lentille divergente O2. Donc...
Ton rayon bleu (mon rayon vert) est trop difficile à exploiter. Je te le déconseille.
Mon rayon bleu arrive sur la lentille divergente L2 en étant parallèle à l'axe optique. Donc...

L'intersection de ces deux rayons donne la position de l'image finale et confirme la valeur trouvée en 2

À toi ! N'hésite pas à avancer par petits pas (un message à chaque pas si tu veux) et à demander de l'aide à nouveau si tu en as besoin.

Posté par
fanfan56re : Images données par 2 lentilles 29-12-14 à 20:07

J'y vais à petits pas, comme tu dis!!

Que représente l'image donnée par L1 pour L2 ?

Pour la lentille convergente L1 : A1B1 est une image réelle
Pour la lentille divergente L2 : A1B1 est...un objet virtuel


Citation :
Calculer la position de l'image finale donnée par L2.

Pas de difficulté particulière :
. Tu connais la relation de conjugaison
. Tu connais également les valeurs de \bar{O_2A_1} et de \bar{O_2F'_2}


\bar{O_2A_1} = OA1 +O1O2 = 130 cm soit 1,3 m
\bar{O_2F'_2}= -0,10m

Posté par
Coll Moderateurre : Images données par 2 lentilles 29-12-14 à 20:24

1)
Oui, pour la lentille divergente L2 A1B1 est bien un objet virtuel

2)
Bravo pour l'écriture des mesures algébriques !
Mais...

\bar{O_2A_1}\,=\,\bar{O_2O_1}\,+\,\bar{O_1A_1}\, \approx\, -0,30\,+\,0,428\,571\, \approx\ 0,128\,571\; \rm{m}
et, en effet :
\bar{O_2F'_2}\,=\,-0,10\;\rm{m}

Il reste à calculer \bar{O_2A_2} avec la relation de conjugaison...

Posté par
fanfan56re : Images données par 2 lentilles 30-12-14 à 09:54

Bonjour Coll,

Je ne sais pas si c'est juste, mais voici ce que j'ai trouvé:

1/ \bar{O_2A_2} = 1/ \bar{O_2F'_2} +1/\bar{O_2A_1} avec \bar{O_2A_1}  = 0,128541m et f' = -0,10 m


1/ \bar{O_2A_2} = 1/0,128571 +1/-0,10 = -2,222196296

1/-2,222196296 = -0,45m

Posté par
Coll Moderateurre : Images données par 2 lentilles 30-12-14 à 09:59



\large \frac{1}{\ \bar{O_2A_2}\ }\;-\;\frac{1}{\ \bar{O_2A_1}\ }\;=\;\frac{1}{\ \bar{O_2F'_2}\ }

Or ici :
\bar{O_2A_1}\,=\,0,128\,571\,\rm{m}
et
\bar{O_2F'_2}\,=\,-0,10\,\rm{m}

On en déduit immédiatement que :

\large \bar{O_2A_2}\;=\;\frac{\ \bar{O_2F'_2}\ \times\ \bar{O_2A_1}\ }{\ \bar{O_2F'_2}\ +\ \bar{O_2A_1}\ }

\large \bar{O_2A_2}\;=\;\frac{\ (-0,10)\ \times\ 0,128\,571}{\ (-0,10)\ +\ 0,128\,571\ }\; =\;-\,0,45\;\rm{m}\;=\;-\,45\;\rm{cm}

Ce qui permet de placer le point A2 sur le dessin (attention au signe ! ! )
Ceci va pouvoir être vérifié avec la construction graphique.

Posté par
fanfan56re : Images données par 2 lentilles 30-12-14 à 10:29

Voici le schéma complété

Images données par 2 lentilles

Posté par
Coll Moderateurre : Images données par 2 lentilles 30-12-14 à 10:59

Très bien !

Voici le mien qui attendait le tien...

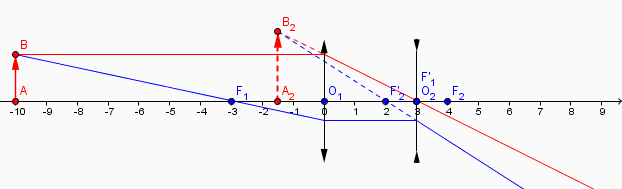
Images données par 2 lentilles

Je trace en traits continus les rayons "réels" et en traits interrompus leurs prolongements ou l'image virtuelle.
Comme pour le précédent graphique, l'unité de distance est le décimètre.

Posté par
fanfan56re : Images données par 2 lentilles 30-12-14 à 12:00

Merci de ton aide, à bientôt!

Posté par
Coll Moderateurre : Images données par 2 lentilles 30-12-14 à 12:09

Je t'en prie.
À une prochaine fois !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !