Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... MasterForum Supérieur de master PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau master
histoire de photons
Posté par artichocacao
yo
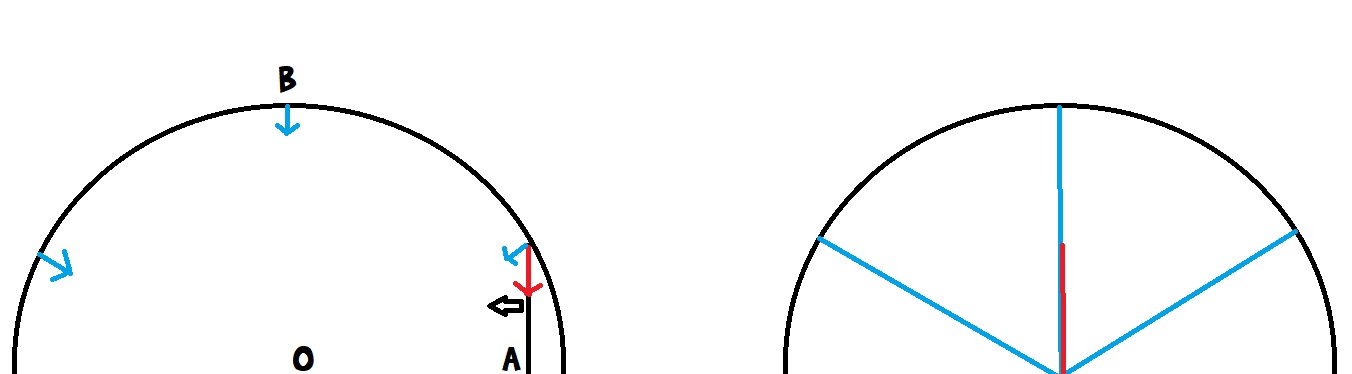
un bâton de longueur L se déplace. Au dessus de lui se trouve une structure circulaire de rayon R d'où partent des photons bleus simultanément de sorte qu'ils arrivent tous en même temps en O
En supposant que le bâton se déplace suffisamment rapidement, un photon parti du haut du bâton (lorsque cette extrémité touche le cercle) arrivera en O lui aussi. Vu qu'il part du même endroit qu'un photon bleu et qu'ils ont la même vitesse, ils doivent alors arriver en même temps
Question: lorsque l'on se déplace avec le bâton, quourpoi voit-on un photon rouge faire un trajet de longueur L et les photons bleu faire un trajet de longueur R arriver et partir en même temps?
Bonjour,
Pourriez-vous préciser votre question ?
Si, à ce que je comprends, le photon part du baton en C (extrémité supérieure du baton) lorsque C touche le cercle, alors le trajet rouge est CO comme le trajet bleu.
c'est vrai que la représentation de droite, vue depuis le bâton, est 'hybride': vu que le bâton se déplace plutôt rapidement, le cercle devrait être représenté comprimé horizontalement. Mais à priori pas verticalement. En tout cas si on considère le relativité d'Einstein. Je voulais surtout représenter la différence de distance parcourue par les photons rouge et bleu
effectivement, le trajet rouge correspond à un trajet bleu partant de C
Mais, du coup, là aussi, si je comprime le cercle façon Einstein, si le trajet rouge doit rester vertical pour représenter le référentiel, le trajet CO n'est pas vertical et reste incliné et de longueur > L...
Finalement, si l'on se place sur le bâton en oubliant que l'on fait parti d'une expérience, il s'agit de comparer le trajet BA avec le trajet CA.
La question est de comparer la simultanéité de l'émission des photons. Pour bien faire, on peut prolonger la longueur du bâton entre C et B et considérer que le photon bleu partant de B déclenche la même horloge que pour le photon rouge (toute la longueur du bâton est criblé d'horloges synchronisées). Puisque les photons bleus partis de B et C arrivent en même temps (dans les référentiels, du bâton ou immobile), les trois photons bleus et rouge arrivent bien en même temps alors que BA!=CA
Citation :
Puisque les photons bleus partis de B et C arrivent en même temps (dans les référentiels, du bâton ou immobile)
Puisque les photons bleus partis de B et C arrivent en même temps (dans les référentiels, du bâton ou immobile)
S'ils arrivent en même temps, comme la longueur du trajet (BO=CO) est la même dans le référentiel du cercle, ils sont partis au même instant dans le référentiel du cercle. B et C étant distincts, dasn le référentiel du baton, l'instant de départ de B est différent de l'instant de départ de C.
Citation :
on peut prolonger la longueur du bâton entre C et B et considérer que le photon bleu partant de B déclenche la même horloge que pour le photon rouge (toute la longueur du bâton est criblé d'horloges synchronisées).
on peut prolonger la longueur du bâton entre C et B et considérer que le photon bleu partant de B déclenche la même horloge que pour le photon rouge (toute la longueur du bâton est criblé d'horloges synchronisées).
Dans ce cas, les départs de B et C sont simultanés dans le référentiel du baton, mais pas dans celui du cercle, les photons n'arriveront donc pas au même instant en O.
pourtant on peut placer des horloges synchronisées dans chaque référentiel de sorte que leur chrono commencent en même temps. Les horloges du bâton seront certes désynchronisées avec celles du cercles en O (lorsque A=O), mais on peut quand même dire que les départs et arrivées sont simultanés à la fois dans le bâton et le cercle
Prenons le problème à l'envers: quand le bâton arrive en A, peut-on déterminer l'emplacement du départ d'un photon arrivant en A (avec un angle alpha) lorsque ledit bâton était à la distance d de A?
Nous connaissons la réponse, qui ne me parait donc pas du tout intuitive, mais que répondre à ceux qui vont dessiner un cercle de rayon L centré sur A et de rayon L, et non R, plus intuitive?
Citation :
on peut quand même dire que les départs et arrivées sont simultanés à la fois dans le bâton et le cercle
on peut quand même dire que les départs et arrivées sont simultanés à la fois dans le bâton et le cercle
Non, mais pour expliquer cela, il faut reprendre toute l'intro à la relativité ; je vais essayer d'écrire quelque chose, mais si quelqu'un veut répondre, je n'ai pas d'objection.
Citation :
quand le bâton arrive en A, peut-on déterminer l'emplacement du départ d'un photon arrivant en A lorsque ledit bâton était à la distance d de A ?
quand le bâton arrive en A, peut-on déterminer l'emplacement du départ d'un photon arrivant en A lorsque ledit bâton était à la distance d de A ?
A préciser. Sinon, il s'est écoulé t=d/v, donc le point de départ est sur un cercle de rayon ct=cd/v, mais j'ai peut-être mal compris, d'où mon "préciser".
Citation :
je vais essayer d'écrire quelque chose
ok
je vais essayer d'écrire quelque chose
je résume: on place en B deux horloges, une se déplace avec le bâton, une sur le cercle fixe, deux autres en C idem, une autre en A au pied du bâton, et une dernière en O, immobile. Les horloges liées au cercle sont synchronisées entre elles. Tout comme les horloges du bâton
Citation :
A préciser
A préciser
effectivement, il faut qu'un photon parcourt la longueur du bâton pendant le trajet de celui-ci. Ceci dit on peut simplifier le problème en demandant où se trouvait le photon qui vient de nous tomber dessus, il y a Xsec. Ne tracerions nous pas un cercle centré sur nous?
Pour le détail, il faut que je mette au point, et de nouveau, "si quelqu'un veut répondre, je n'ai pas d'objection."
Citation :
On peut simplifier le problème en demandant où se trouvait le photon qui vient de nous tomber dessus, il y a Xsec. Ne tracerions nous pas un cercle centré sur nous ?
On peut simplifier le problème en demandant où se trouvait le photon qui vient de nous tomber dessus, il y a Xsec. Ne tracerions nous pas un cercle centré sur nous ?
Oui, le photon se trouvait, X sec avant, sur une sphère centrée sur nous de rayon
Citation :
une sphère centrée sur nous de rayon R=X \cdot c.
une sphère centrée sur nous de rayon R=X \cdot c.
du coup tu confirmerais que, sur le schéma, l'on dessinerait un cercle centré sur O et de rayon L et non R. L'écoulement du temps est représenté par le trajet vertical du photon rouge le long du bâton
Si le cercle de rayon R est compressé dans le sens de la direction, on signifierait que la vitesse a tendance à compresser l'espace devant lui. Par extension&symétrie, l'espace a tendance à se dilater derrière lui
Si l'on veut que les photons arrivent à c sur le bâton, la seule possibilité est de considérer que l'écoulement du temps subit le traitement inverse, c'est ce que raconte le modèle de Lorentz, pas celui d'Einstein: le temps en avant est alors dilaté. Par exemple un pilote voit une histoire en accéléré devant lui, et au ralenti derrière lui
Quand on s'échappe de la Terre, nous la voyons au ralenti, redshifté e, sombre et allongée. Quand on revient, on la voit en accéléré, blueshifté, lumineuse et aplatie comme une crêpe. C'est ce que dirait l'observation, et on est tous d'accord là dessus
Avec le modèle de Lorentz, on pourrait alors reconstruire le cercle de rayon R en fonction de c, v, L
On compare les résultats avec le modèle d'Einstein?
Citation :
nous la voyons au ralenti, redshifté e, sombre et allongée
comme un ballon de rugby pointé vers nousnous la voyons au ralenti, redshifté e, sombre et allongée
On s'éloigne du sujet initial : le red/blue shift, lumineux/sombre ... ne change rien au problème.
Dans le référentiel du baton, les deux rayons issus de C arrive bien après un temps de parcours de L/c. Mais le rayon issu de B arrive bien en même temps : il a parcouru une distance plus grande mais a été émis avant.
Citation :
On s'éloigne du sujet initial : le red/blue shift, lumineux/sombre ... ne change rien au problème.
On s'éloigne du sujet initial : le red/blue shift, lumineux/sombre ... ne change rien au problème.
C'était pour pousser le raisonnement, pour voir jusqu'où il mène. Tant qu'il reste cohérent, tant qu'il n'amène pas de contradictions, tant qu'il permet de se comparer à la problématique (le modèle d'Einstein étant une approximation potentielle voire probable du modèle de Lorentz), cela reste à son avantage
Je ne cherche pas à défendre nécessairement le modèle, mais il doit au moins ne pas exhiber de contradictions, si tant est qu'on veuille qu'il en résolve
Citation :
il a parcouru une distance plus grande mais a été émis avant.
il a parcouru une distance plus grande mais a été émis avant.
Et bien ça se discute. La possibilité de placer des horloges synchrones semble raconter une autre histoire. S'il faut retenir les infos apportées par les photons, il faut aussi considérer le comportement local, deux informations complémentaires. C'est ce que permet de résoudre le modèle de Lorentz, en combinant le comportement des photons en tant que sonde de la géométrie qui nous sépare d'un évènement, et le comportement temporel local de cette géométrie le long de son trajet
Si, à nous deux, nous désirons que les photons se déplacent à c alors que des horloges pourraient indiquer que non, le seul compromis est de compresser l'espace. Et le modèle d'Einstein ne serait-il qu'une approximation du modèle de Lorentz, celui-ci étant plus à même de décrire la réalité?
Ensuite, on peut se demander jusqu'où irait cette approximation, tout comme on peut aussi se pencher sur le modèle de Lorentz, sur la notion de référentiel absolu? Son seul candidat est l'univers observable, il a certes la particularité d'être toujours centré sur nous, donc pas spécialement immobile, mais il nous présente le dipôle cosmologique. Celui-ci, rappelons-le, exprime notre vitesse relativement à lui, nous racontant l'histoire de notre inertie locale (puisque cette mesure est nécessairement issue de la moyenne des décalages vers le rouge de la matière proche, lointaine, très lointaine, très très lointaine..)
Et cette histoire me parait du coup candidate pour donner un sens à des mystères cosmiques observés. Si l'on considère l'écoulement du temps by l'univers observable, assez distant notamment, on peut penser qu'il n'a rien à voir avec celui de notre galaxie, qu'il peut se former une tension, une tension supplémentaire entre ces deux entités, notamment à leur "frontière commune": la matière noire pourrait donc n'être qu'un effet produit par le modèle jouet d'Einstein
En plus d'aider à la compréhension de notre géométrie, le modèle de Lorentz pourrait permettre de combler des lacunes du modèle actuel. On aurait tord de se braquer uniquement sur le modèle d'Einstein, dont on a de toute façon tordu le coup depuis quelques temps déjà (la dilatation cosmique de l'espace, qui n'a énergétiquement aucun sens, des phénomènes plus rapides que la lumière, des mesures invérifiables..)
Je ne sais si je suis convaincu moi-même, mais ce raisonnement parait convainquant, non?
Citation :
tordu le coup
tordu le coup
on peut encore tordre le cou à Lorentz, mais ce sera plus difficile. De toute façon on lui a tout de suite tordu le cou dès le départ, on s'est tout de suite jeté sur la seule hypothèse d'Einstein, la constance universelle de c en toute circonstance, bien plus commode. Donc on arrête de tordre le cou du modèle d'Einstein, il a fait son taf, et on remet celui de Lorentz en place. Et, pour le coup, on peut commencer à taper bas, pour voir ce qu'il a dans le ventre, tout en s'empêchant les coups bas
mince, je me rends compte que je me suis gouré de forum, je croyais que j'étais dans la section poésie
Citation :
Je ne sais si je suis convaincu moi-même, mais ce raisonnement parait convainquant, non ?
Je ne sais si je suis convaincu moi-même, mais ce raisonnement parait convainquant, non ?
Si vous vous êtes convaincu vous-même, c'est le plus important.
Citation :
Si vous vous êtes convaincu vous-même, c'est le plus important
Si vous vous êtes convaincu vous-même, c'est le plus important
je pose la question de l'éventuelle pertinence du modèle de Lorentz, mais il y a d'autres questions à lui poser pour le tester (je pense notamment au champs électromagnétique), surtout si je donne l'impression d'avoir chercher à prêcher pour lui( alors que j'ai tout autant cherché à le contredire)
Disons qu'on pourrait ouvrir un nouveau sujet mais bon, il s'agit d'un modèle abandonné, non travaillé donc on est surement borderline avec la Charte
Ma foi, j'ouvre une fenêtre, à mon avis il n'y en aura pas beaucoup d'autres, surtout si l'on s'attend à ce que les expériences qui discrimineraient les deux modèles (Einstein et Lorentz) sont forcément peu nombreuses (après tout un référentiel absolu n'empêche pas la relativité de mesures faites les unes par rapport à d'autres). Je pense toutefois que l'expérience citée ici, même si de pensée (potentiellement difficilement réalisable si elle demande à atteindre de grande vitesse pour être mesurable), amène à la falsifiabilité du modèle et donc à des partisans. Son énoncé est de plus assez clair et non ambigu, et le modèle de Lorentz est encore vierge de toute déformation, ce que l'on peut reprocher au modèle actuel, sorte d'hybride Einstein-Lorentz (surtout du point de vue cosmologique)
J'en fais des caisses, j'attends sûrement qu'on en fasse des caisses pour me faire comprendre que je raconte n'importe quoi. Sans commander quiconque hein
Je reprends...
Je m'étais arrêté à "Je ne sais si je suis convaincu moi-même" qui veut souvent dire "je suis convaincu".
Je voulais de l'aide parce qu'il est difficile de répondre en dix lignes dans un forum ce qui nécessite 13 pages dans le lien que je vous ai indiqué.
D'autre part, j'ai bien écrit qqch mais qui ne va peut-être pas passé, j'essaie :
PDF - 64 Ko
Citation :
pdf
ligne 5&6: si le photon avait été émis au milieu d'un wagon, il aurait atteint l'avant et l'arrière en même temps dans le référentiel du wagon. Quourpoi les temps calculés sont différents? Par symétrie, les extrémités du quai ne seraient donc pas atteintes en même temps par un photon émis dans le wagon?
Avec la relativité by Einstein, on parle de défaut de synchronicité lorsque l'on regarde deux évènements depuis un point de vue différent
Il y a un deuxième phénomène de synchronicité, lorsque l'on considère des horloges synchrones d'un même référentiel et il est incompatible avec la présentation by Einstein: lorsque l'on sort du wagon que ce soit à l'arrière ou à l'avant, l'horloge de l'avant et de l'arrière afficheront le même décalage avec les horloges du quai: ce qui est synchrone dans le train l'est aussi sur le quai, pas à la même date certes, mais synchrone
Donc, normalement, que l'on prenne deux photons partis du milieu du quai ou du wagon, on devrait observer la même chose, ce n'est clairement pas le cas avec Einstein. Si l'on veut la synchronicité à la fois dans le wagon et sur le quai, il faut considérer, dans le référentiel du quai que les photons émis dans le wagon ne se déplacent pas à c, mais à c+v et c-v, et que le wagon est allongé (les photons atteignent les extrémités du wagon après ceux du quai si l'on veut que le temps s'écoule plus rapidement sur le quai) de façon à constater le décalage identique à l'arrière et à l'avant
Le modèle de Lorentz résume mieux la chose en supposant que dans le wagon il se produit deux phénomènes (temps et espace) concomitants qui s'opposent de façon à garder la vitesse de la lumière constante dans le wagon. Cette explication ne suffit pas pour expliquer que le trajet des photons émis depuis le quai n'est pas impacté par ces phénomènes, quand bien même ils traverseraient le wagon. Si le modèle d'Einstein est une approximation du modèle de Lorentz, plus à même de décrire la réalité, celui-ci est lui-même une approximation d'un autre modèle, plus proche encore de la réalité
Pour les histoires de wagon (Un photon émis au milieu d'un wagon atteint l'avant et l'arrière en même temps dans le référentiel du wagon mais pas dans celui du quai) : 
Et idem pour non à :
Citation :
lorsque l'on sort du wagon que ce soit à l'arrière ou à l'avant, l'horloge de l'avant et de l'arrière afficheront le même décalage avec les horloges du quai: ce qui est synchrone dans le train l'est aussi sur le quai, pas à la même date certes, mais synchrone
lorsque l'on sort du wagon que ce soit à l'arrière ou à l'avant, l'horloge de l'avant et de l'arrière afficheront le même décalage avec les horloges du quai: ce qui est synchrone dans le train l'est aussi sur le quai, pas à la même date certes, mais synchrone
Comme déjà dit, difficile de répondre en dix lignes ce que le texte met, disons les 5 premières pages, à mettre en place.
SI vous cherchez un ouvrage simple : "L'Univers en perspective, Relativité restreinte" Jean Marie Vigoureux
Je ne sais trop ce que vous appelez modèle de Lorentz, si ce sont les transformation de Lorentz, elles donnent les mêmes résultats, si c'est l'interprétation, si vous préférez, très bien.
La réalité est très bien décrite par l'un ou l"autre.
Entendons-nous bien: si les photons sont émis sur le quai, ils reviendront (via des miroirs aux extrémités du quai) au milieu. S'ils sont émis dans le train, ils reviendront (via des miroirs aux extrémités du train) au milieu du train. A priori le milieu du train n'a aucun rapport avec le milieu du quai, mais l'expérience devrait être faite pour savoir s'ils peuvent coïncider. A priori les calculs disent que c'est impossible, mais avec le modèle de Lorentz, ça devrait être possible
Citation :
non
non
si. qu'une horloge soit placée à l'avant ou à l'arrière, elle accusera le même retard par rapport aux horloges du quai, du au fait qu'elles étaient toutes deux en mouvement à la même vitesse. Je suis sûr que tes références en parlent (une horloge en mouvement subit un décalage) tout comme elle propose les mêmes calculs que toi, sans relever le problème, par exemple en considérant des photons émis dans le train plutôt que sur le quai
quand on est dans le train, on observe que les photons arriveront en même temps à l'avant et à l'arrière, et quand on est sur le quai on observera la même chose. Dans le même temps, lorsque les photons atteignent les extrémités du train, l'un a dépassé une extrémité du quai, l'autre ne l'a pas encore atteinte
Il y a nécessairement une contradiction, que toi tu résous en désynchronisant les horloges du train. Désolé pour toi, mais les horloges se déplacent à la même vitesse, elles subissent donc le même décalage et restent synchrones
on est obligé de faire les hypothèses suivantes:
Soit la vitesse de la lumière est impactée par la vitesse du référentiel d'où le photon est émis. Il me semble qu'il n'y a pas de mesures qui l'infirment, mais de toute façon, les photons émis sur le quai ou dans le train n'auront pas le même comportement. On peut écarter cette hypothèse
Soit on dit que l'espace et le temps ont des comportements
complémentaires (l'un contracte quand l'autre dilate) et concomitants de façon à ce que la vitesse de la lumière reste constante. C'est le modèle de Lorentz, dont le modèle d'Einstein en est une approximation et il y a nécessairement des expériences qui les discriminent
Je supprime le dernier paragraphe de mon dernier message, en fait cette hypothèse est la plus à même de répondre aux observations: une même paire de photons, qu'ils soient émis dans le train ou sur le quai, resteront synchrones, seules des déformations d'espace et de temps peuvent permettre de voir des photons synchrones depuis le train mais pas aux extrémités du quai (vu que le photon qui va vers l'avant atteint une extrémité du quai avant l'autre, alors que sur le quai ils atteignent bien les extrémités du quai simultanément), ou depuis le quai mais pas aux extrémités du train (idem l'arrière du train est atteinte avant l'autre, alors que dans le train, les extrémités sont atteintes en même temps)
Bref, je peux vous accorder que les évènements sont en apparence non synchrones. Mais en apparence seulement
Si les deux modèles d'Einstein et de Lorentz décrivent bien la réalité, il est cependant inconcevable de garder les deux. A un moment donné, il faudra trancher
PS: dans votre exemple, les photons atteignent des endroits distincts. Ce qui revient au même que de comparer avec l'exemple travaillé ici (bâton en marche arrière), cependant mon exemple fait intervenir la 2D, et elle joue un rôle (contraction dans une direction, pas forcément dans l'autre). Prière de ne pas trop diverger!
Bonjour gts2, bonjour archicacao
Citation :
(gts2) Je ne sais trop ce que vous appelez modèle de Lorentz,
(gts2) Je ne sais trop ce que vous appelez modèle de Lorentz,
C'est la théorie de l'éther de Lorentz, je pense, de même que "le modèle" d'EInstein, c'est la RR en fait ! (si j'ai bien suivi)
Et archicacao cherche encore laquelle des théories est la bonne. Les physiciens ont tranché depuis longtemps mais il hésite encore, apparemment.
bonjour krinn, je peux concevoir qu'on est archi fan de chocolat, plus que pour une recette à base d'artichaud et de cacao. Quoique, l'artichaud est un peu sucré, ça peut peut-être le faire!
Citation :
C'est la théorie de l'éther de Lorentz
C'est la théorie de l'éther de Lorentz
Je ne sais de quelle hypothèse est parti Lorentz: soit la constance de la vitesse de la lumière s'explique à travers la concomitance/complémentarité d'effets en temps ou en espace et ceci ne peut s'expliquer qu'en supposant un éther, ou si l'éther est d'abord supposé et nécessite ces effets, après tout c'était surtout la question de l'éther qui était posée, pas celle de la constance. Einstein fait un raccourci en supposant cette constance, il n'explique pas comment elle est obtenue. A priori c'est une hypothèse grossière, par exemple quand on prend deux référentiels ayant des vitesses différentes par rapport à un troisième, il devient hasardeux de considérer un photon de l'un se déplaçant dans l'autre (le cas de la paire de photon traversant un train dans un sens (-v) et dans l'autre (v) y fait référence), on peut éventuellement en proposer un nouveau sujet
Citation :
Et archicacao cherche encore laquelle des théories est la bonne
Et archicacao cherche encore laquelle des théories est la bonne
Je me trouve effectivement à discuter de ces modèles, et comme ces messages le montrent, la nuance que ces deux modèles peuvent apporter est (naturellement) faible. On est tous en droit de penser que si un nouveau modèle doit remplacer celui d'Einstein, il devra inclure ce dernier d'une façon ou d'une autre
Si mon hypothèse, à savoir que le modèle d'Einstein est une approximation du modèle de Lorentz, est universelle, alors elle est potentiellement la réponse
Citation :
Les physiciens ont tranché depuis longtemps mais il hésite encore, apparemment.
Les physiciens ont tranché depuis longtemps mais il hésite encore, apparemment.
Si on creuse, on entend plutôt dire que les deux modèles sont équivalents, un peu comme de dire que l'expansion de l'univers est équivalent à un univers statique dans lequel les évènements s'échappent à des vitesses folles (c'est l'hypothèse de départ avec v=H.d, sachant que ce modèle arrive même à c ~H.R, R étant le rayon de l'horizon cosmologique). Cette équivalence est sans doute bonne mais là aussi c'est une hypothèse pour construire un modèle, qui souffre dans les deux cas d'un problème d'énergie (création d'espace vide dans l'un, 'impulsion relative continue' dans l'autre, au moins dans une équivalence les résultats sont équivalents, même lorsqu'ils sont négatifs). On se penche sur le problème énergétique que pose l'accélération de l'expansion, on devrait avant cela se pencher sur l'énergie demandée par la 'simple' expansion. Il faut garder ça en tête pour pouvoir éventuellement rétropédaler sur ce qui peut ressembler à des acquis
Dans la tête des physiciens qui considèrent cette équivalence (Lorentz-Einstein), il n'y a plus qu'à suivre l'hypothèse d'Einstein, à savoir la vitesse de la lumière est constante en toute circonstance. Après tout, quourpoi s'emmerder avec le modèle de Lorentz si, de l'autre côté, il suffit de considérer que "les photons se déplacent à c, point".
Pourtant, il est clair que ces modèles ne sont pas équivalents, par exemple on en discute dans l'[url=https://www.ilephysique.net/sujet-relativite-et-photons-331074.html]autre fil[/url], le principe de relativité ne peut être valable qu'en prenant en compte l'accélération propre. La seule connaissance des vitesses est insuffisante pour déterminer qui, des deux jumeaux, sera le plus vieux, il est nécessaire de savoir qui a pris de la vitesse. Dans le paradoxe des jumeaux, on s'attache à l'âge des participants. Cependant, on peut résumer l'expérience en considérant deux vaisseaux, un faisant l'aller, un autre faisant le retour. Lorsqu'ils se croisent, plutôt que de transférer le pilote, on transfère l'info de l'horloge et peut alors comparer les évolutions temporelles. Là aussi on peut ouvrir un nouveau sujet (avec trois vaisseaux), on peut avoir des configurations équivalentes (à base de vitesses relatives) mais des résultats différents
Le principe de relativité a de tout façon un coup dans l'aile depuis l'expérience de Hafle&Keating, au bout de laquelle on devait s'attendre au même différentiel temporel pour les deux avions. Là aussi il faut considérer l'accélération (centrifuge), et non les seules vitesses par rapport au sol. Par contre si on me dit que les vitesses sont absolues car relatives aux accélérations centrifuges, absolues, je ne serais pas contre. Par exemple, j'ai déjà regardé les calculs, il n'y a pas spécifiquement des termes en m.v²/R, mais il y a bien v² (sans racine) et il faut normaliser l'équation par M/R. Si tu veux, on peut ouvrir un nouveau fil (on peut trouver les résultats p12 du document hafelekeating175-analyse.pdf à trouver sur un moteur de recherche)
Dans ce fil, ce n'est pas le principe de relativité qui est questionné mais la constance universelle de la vitesse de la lumière, expliquant à elle seule qu'il faut tracer un cercle de rayon L et non R
A mon sens, il y a suffisamment d'éléments pour que l'on se penche sur le modèle de Lorentz. J'affirme que ce modèle a été abandonné pour des raisons de commodité (on ne va pas se le cacher, des photons qui se déplacent tout le temps à c, c'est bien pratique) en pensant que les deux modèles sont équivalents. Si ce n'est pas le cas, si on suppose que les deux modèles ne sont pas équivalents et si on suppose que le modèle d'Einstein est plus proche de la réalité que celui de Lorentz, alors le travail n'est pas fini, il faut les discriminer. Si personne n'a sorti d'expériences les discriminant, cela signifie qu'on est resté dans cette idée d'équivalence, ou alors qu'elles demandaient une précision de mesure trop importante. Je n'ai pas spécialement creusé, mais je n'ai jamais entendu parler de ce genre d'expérience. La commodité de l'hypothèse de la constance de c en toute circonstance, des résultats qui ne permettent pas de falsifier le modèle d'Einstein (sans pour autant falsifier celui de Lorentz, on peut en effet s'attendre à ce que des mesures relatives à d'autres ne soient pas altérées par la présence d'un référentiel absolu, après tout on peut faire des mesures relatives sans passer par O) n'ont pas aidé et font qu'on est naturellement resté sur le modèle d'Einstein
Bon, maintenant que le modèle d'Einstein a été bien poncé, on pourrait se pencher sur celui de Lorentz, après tout il est assez proche du modèle d'Einstein, et on ne sait pas s'ils sont équivalents ni lequel des deux est plus proche de la réalité. Et si on voulait, à nouveau, extrapoler le modèle, on pourrait même expliquer des mystères cosmologiques (comme la matière noire, cf le message 29-03-25 à 03:28). Entre les problèmes que je souligne et son potentiel, on aurait tord de s'en priver...
Cela part un peu dans tous les sens :
Pour Hafele et Keating, l'hypothèse est que les référentiels sont quasi galiléen (d'où le choix du référentiel géocentrique et non terrestre) et donc uniquement la prise en compte de , c'est de là d'où vient le v2. Et je ne vois pas de coup dans l'aile, puisqu'ils retrouvent les résultats des jumeaux de Langevin.
Je reviens sur ma question, qu'entendez-vous par Lorentz ?
- si c'est, comme l'indique krinn, uniquement l'interprétation en terme d'éther pourquoi pas (cf. la commodité de Poincaré)
- si ce sont les calculs, comme les transformations de Lorentz vues par Lorentz ont beaucoup varié, auxquelles faites-vous référence ? Si c'est cela, il n'y a pas photo : : comme dit krinn "les physiciens ont tranché depuis longtemps".
Pour la cosmologie, il faut tenir compte de la gravitation et le modèle gravitationnel de Lorentz n'a pas été bien loin.
Citation :
uniquement la prise en compte de \sqrt{1-v^2/c^2}, c'est de là d'où vient le v2
uniquement la prise en compte de \sqrt{1-v^2/c^2}, c'est de là d'où vient le v2
Dans le doc, je vois un v² plutôt qu'un facteur de Lorentz..
Citation :
Et je ne vois pas de coup dans l'aile
Et je ne vois pas de coup dans l'aile
A partir du moment où le principe de relativité nous dirait que les avions, en déplacement identique à l'est et à l'ouest, subiront les mêmes affres du temps, les résultats ne lui donnent pas raison...
Citation :
puisqu'ils retrouvent les résultats des jumeaux de Langevin
puisqu'ils retrouvent les résultats des jumeaux de Langevin
ben non, un avion est plus jeune que le sol (le voyage ne s'est pas fait dans le passé comme dans superman, le sol a continué à évoluer..), l'autre est plus vieux
Citation :
Je reviens sur ma question, qu'entendez-vous par Lorentz ?
- si c'est, comme l'indique krinn, uniquement l'interprétation en terme d'éther pourquoi pas (cf. la commodité de Poincaré)
Je reviens sur ma question, qu'entendez-vous par Lorentz ?
- si c'est, comme l'indique krinn, uniquement l'interprétation en terme d'éther pourquoi pas (cf. la commodité de Poincaré)
le problème c'est qu'aucun éther n'a été identifié, est-ce l'univers observable etc? On s'est tout de suite jeté sur l'hypothèse d'Einstein et on s'est évité cette question. Par simple commodité donc
Citation :
- si ce sont les calculs, comme les transformations de Lorentz vues par Lorentz ont beaucoup varié, auxquelles faites-vous référence ?
- si ce sont les calculs, comme les transformations de Lorentz vues par Lorentz ont beaucoup varié, auxquelles faites-vous référence ?
à partir du moment où on n'a pas le référentiel, les calculs deviennent hasardeux.. On peut essayer de jouer aux devinettes à partir du modèle d'Einstein, par exemple il y a un truc qui me chiffonne avec ce modèle quand on dit que depuis le vaisseau, la Terre est contractée, et réciproquement. Naïvement, on aurait pu parler de la symétrie "vaisseau contracté <=> terre dilatée", mais la symétrie n'est pas là, on l'observe plutôt sur un A/R en parlant de dilatation à l'aller (Terre allongée), contraction au retour (Terre aplatie). Je me base sur des "observations de pensée". Le modèle actuel considère que la contraction est à la fois à l'aller et au retour, premier point. Deuxième point: seule la Terre ou le vaisseau subissent un effet spatial, considérant sans doute que le vide entre le vaisseau et la Terre a un statut spécial car dépourvu de référentiel matériel, d'où le questionnement que l'on peut voir sur l'intérêt que peut avoir la présence d'un lien matériel entre des sondes parsemant un trajet dans le vide, ou entre deux fusées identiques se poursuivant. Dans le modèle de Lorentz, l'espace dans la direction de mouvement est contracté tandis qu'il est dilaté dans la direction opposée. Quand un vaisseau parcourt le trajet Terre Andromède en 3sec de temps propre, l'espace Terre-Andromède est contracté de telle sorte qu'en 3sec, le vaisseau recevra les photons émis pendant 6Ma par Andromède. En gros le vaisseau va fondre, les photons seront en grand nombre et transportés dans le domaine gamma, du coup si on fait l'analogie avec la friction de l'air, le 'référentiel absolu' serait aussi bête que l'univers observable, que l'on définit grâce aux photons. Ce référentiel est remarquable: il a le statut relatif (centré sur nous, il se déplace avec nous) mais aussi absolu (présence du CMB). J'ai d'autres hypothèses concernant cet univers observable (mais autant dire qu'il va falloir me pousser à bout pour les sortir), qui le distingue de sa conception actuelle, mais je pense que l'on peut déjà s'entendre sur ce à quoi peut ressembler le référentiel absolu nécessaire au fonctionnement du modèle de Lorentz
Citation :
Pour la cosmologie, il faut tenir compte de la gravitation et le modèle gravitationnel de Lorentz n'a pas été bien loin
Pour la cosmologie, il faut tenir compte de la gravitation et le modèle gravitationnel de Lorentz n'a pas été bien loin
Lorentz a-t-il, dans ses 'mémoires', fait référence à un quelconque univers observable? Pas dit qu'à l'époque sa conception était éventualisée, et encore moins le CMB...
Citation :
Quand un vaisseau parcourt le trajet Terre Andromède en 3sec de temps propre, l'espace Terre-Andromède est contracté de telle sorte qu'en 3sec, le vaisseau recevra les photons émis pendant 6Ma par Andromède
Quand un vaisseau parcourt le trajet Terre Andromède en 3sec de temps propre, l'espace Terre-Andromède est contracté de telle sorte qu'en 3sec, le vaisseau recevra les photons émis pendant 6Ma par Andromède
oups. il fallait lire "pendant 3Ma". C'est lors du retour Andromède-Terre, que le vaisseau recevra les photons émis par la Terre pendant 6Ma (à l'aller le vaisseau en reçoit très peu). 6Ma, +/- des pouillèmes donc (le vaisseau ne va pas exactement à la vitesse de la lumière). Le trajet est idéalisé, sans accélération, un vaisseau va sur Andromède et y croise le vaisseau retour. Pour bien faire, il faut élargir le domaine d'étude à partir du temps où les vaisseaux se mettent à accélérer (et du coup, plutôt que de faire dépasser la Terre au vaisseau, celui-ci peut partir de celle-ci). Là on pourra considérer les photons reçus pendant la période de freinage, si la décélération jusqu'à vitesse nulle (par rapport à la Terre) est obtenue en 1000ans de temps propre, le vaisseau recevra les photons qu'il aurait du recevoir à l'aller, soit 3Ma d'évolution de la Terre. bref
Pour décrire la brisure de symétrie du à l'accélération: à l'aller, pour que le vaisseau reçoive un bip par seconde, il faut que la Terre émette une rafale de bips juste après son passage sur une période ultra courte, le vaisseau les recevra à 1, 2 et 3Ma. Tandis que si le vaisseau émet un bip/sec, la Terre les recevra au bout de 1, 2, 3Ma. J'ai l'impression que pour résoudre le paradoxe des jumeaux, en plus de devoir parler d'accélération, il faille parler d'un troisième référentiel (ici Andromède) que l'on va même devoir étendre à l'univers observable. En effet les photons et vaisseaux n'empruntent pas le seul trajet spatio-temporel qui sépare Andromède et la Terre, mais, aux faibles accélérations (entre le bord de la voie lactée et le bord d'Andromède), un trajet dans "l'univers observable". Je ne peux pas être plus précis, mais après tout, lors du trajet, on a beau viser Andromède, sa masse, son champs gravitationnel, à la vue de la distance (son champs gravitationnel est faible) et sa masse (faible devant l'univers observable) on est surtout en train de viser la moitié de l'univers observable, sa masse, son champs gravitationnel. Il pourrait être intéressant d'ouvrir un nouveau sujet sur l'évolution du temps au centre de la Terre: le champs gravitationnel y est en apparence nul (on flotterait) mais le temps s'y écoule quand même. Par contre, on n'a pas réussi à me convaincre pour savoir s'il s'écoulait plus rapidement ou lentement qu'à la surface, une histoire de champs vs potentiel gravitationnel, je suspecte un biais d'observation. Si on ne considère que le potentiel gravitationnel, y a-t-il déjà eu une évaluation de celui de l'univers observable? Peut-on le comparer avec celui de la voie lactée? Réciproquement, peut-on simuler les potentiels gravitationnels (peu importe la forme de celui de l'univers observable, on fait varier les paramètres d'évolution jusqu'à obtenir gain de cause) afin d'obtenir un 'effet matière noire' sur le bord des galaxies?
Pas besoin de répondre à ces questions, je souligne juste qu'elles peuvent devenir légitimes dans le cadre du modèle de Lorentz. Dans le modèle d'Einstein, l'univers observable n'est qu'une curiosité, un trajet Terre-Andromède ne considérera que l'évolution des champs gravitationnels locaux (Terre, Soleil, voie lactée, Andromède), quand bien même on se trouve à bonne distance (au milieu du trajet, le point de vue local devient hasardeux, je trouve), où l'espace est considéré plat et donc sans évolution temporel (du moins il s'envolerait sur Terre comme sur Andromède). A priori, à partir d'une certaine distance à une galaxie, aux faibles accélérations donc, ce n'est plus la galaxie qui impose une évolution temporelle en rapport avec la distance, mais l'univers observable. Une autre image, ce serait le photon qui passe la surface de la Terre, qui serait blueshifté jusqu'à une certaine distance (la séparation coeur-manteau il me semble) puis redshifté. Si celui-ci n'est pas redhifté jusqu'à f=0 au centre de la Terre, c'est que celui-ci subirait encore le champs du Soleil, de la voie lactée, de l'univers observable. Bref
Désolé pour tous ces apartés, mais il faut bien chercher une physique cohérente de bout en bout...
Citation :
je vois un v² plutôt qu'un facteur de Lorentz.
je vois un v² plutôt qu'un facteur de Lorentz.
Le facteur de Lorentz (modifié par la gravitation est à la page précédente (p 11), et il y a un DL
Citation :
les résultats ne lui donnent pas raison...
les résultats ne lui donnent pas raison...
Pour faire l'étude, ils prennent un référentiel inertiel (géocentrique) et ils utilisent des triplés plutôt que des jumeaux : l'horloge géocentrique n'étant pas facile à observer, il observe trois horloges : la terre à la vitesse Rω (1), un avion à Rω+v (2) et un autre à Rω-v (3) et ils comparent deux triplés 1-2 ou 1-3.
Citation :
les calculs deviennent hasardeux.
les calculs deviennent hasardeux.
Dans ce cas, on ne peut rien faire : la physique se repose sur deux béquilles les maths et l'expérience : on "invente" une expérience, on fait les calculs, on en déduit des résultats numériques (maths) puis on compare ces résultats à l'expérience. Si on ne fait pas cela, la physique d'Aristote marche très bien, pas la peine d'aller plus loin.
Citation :
Tandis que si le vaisseau émet un bip/sec, la Terre les recevra au bout de 1, 2, 3Ma.
re oups, évidemment. on les recevera au bout de 2, 4, 6Ma (le temps que le vaisseau atteigne 1Ma, plus le temps de trajet du premier bip 'écho', résultat de l'écho du bip envoyé par la Terre sur le vaisseau, alors situé à 1Ma de la Terre, ça fait 2Ma)
Tandis que si le vaisseau émet un bip/sec, la Terre les recevra au bout de 1, 2, 3Ma.
Bon euh bref, c'était pour parler de l'antisymétrie provoquée par l'accélération. Sur Terre, à T=6Ma on reçoit une rafale ultra courte de bips, juste avant l'arrivée du vaisseau. Là aussi sans histoire d'accélération. Bon bref hein
Sinon, je trouve qu'on est sur la bonne voie, j'ai l'impression que le calcul pour montrer que le cercle à tracer a un rayon R ou L n'est pas convaincant, et que du coup on parle du modèle de Lorentz. Sinon, y a-t-il, existe-t-il, une autre raison, un autre modèle expliquant la contradiction portant sur la dimension du cercle? je ne voudrais pas paraître comme ayant un fantasme quelconque sur ce modèle, c'est juste qu'il pourrait permettre de "coller des bouts" un peu mieux, non?
Citation :
il y a un DL
il y a un DL
sauf que le "1" ne compte pas (na), il n'offre aucune information supplémentaire entre dt et dt', les termes à comparer sont donc le champs de gravitation et le terme en v², ce qui se comprend dans l'équation p12. On comprend que l'équation peut être normalisée par le facteur R/M et que l'on compare un champs gravitationnel et un champs d'accélération (centrifuge)
On peut toutefois dire (à partir de l'eq p12) "ah, on pourrait y voir un dl en ajoutant un 1", mais alors cela signifie que l'eq p12 est en fait exacte au lieu d'être approximative. et c'est l'eq p11 qui devient approximative... Ma foi les modèles d'Einstein et de Lorentz savent se recouper assez bien, il faut l'admettre. Poussons donc le raisonnement
A ce moment là, on ne peut plus considérer un vecteur vitesse sans considérer les accélérations centrifuges, en somme un mouvement dans l'univers correspond surtout à un ensemble immense d'accélérations centrifuges centrées sur les galaxies (en arrondissant, hein, on n'est pas à un atome près), d'où l'analogie au centre de la Terre. Et l'application champs univers vs galaxie
A suivre donc...
sinon, tu peux éventuellement me souligner qu'il y a aussi un "2" dans l'équation p12 et me demander d'expliquer d'où il vient s'il ne venait pas du dl du facteur de Lorentz. Bof, soit ça signifie quelque chose sur la géométrie (dt, v, R), la masse, soit je le fais disparaître et fait apparaître des 2 ou des racines de 2 ailleurs, par exemple dans le facteur de normalité, dans la constante gravitationnelle? On peut s'attendre à ce que le modèle de Lorentz, écrit avec des mathématiques dédiées au modèle d'Einstein, puisse paraître inélégant au bout d'un moment (ouai, c'est vite dit parceque quand c'est le modèle d'Einstein qui devient inélégant, on fait du Lorentz, et plutôt même du simili Lorentz, pas assumé donc). Cependant, on gagnerait un atout non négligeable: plutôt que de bosser avec du v² sous racine, nous n'aurions plus qu'à bosser avec des v². Si tu as fait un peu de physique relativiste, tu comprends ce que je veux dire. D'ailleurs je pense que tu viens à l'instant de basculer vers le modèle de Lorentz, c'est ça le pouvoir de la commodité des hypothèses, tant qu'elles peuvent permettre de simplifier naturellement les calculs, on prend!
Citation :
Pour faire l'étude
Pour faire l'étude
j'entends bien. Le modèle d'Einstein peut toujours défendre sa peau. Cependant, à un moment de votre raisonement, je serai capable de vous rappeler que le principe de relativité n'est pas observé. Par exemple dans votre réponse, votre calcul indique v+Rw et -v+Rw, Ce n'est clairement pas le principe de relativité, car lorsque je suis au sol au décollage des avions, je vois un avion à v et un autre à -v. De mon point de vue, j'applique le principe de relativité et alors les avions devront revenir avec le même décalage temporel. L'univers observable n'a rien à voir là-dedans. Maintenant, si tu écris RW+/v, tu es en train de supposer un référentiel absolu (pour des mouvements circulaires, soit), mais un référentiel absolu tout de même. Et j'imagine qu'on peut l'étendre avec des termes concernant le Soleil, la Lune, la voie lactée, voire ... l'univers observable? Ok, ben.. je prends! Et ça a l'air de marcher mieux que le principe de relativité
Citation :
deux béquilles les maths et l'expérience
deux béquilles les maths et l'expérience
Bon, sinon, j'estime que nous avons tout deux défendu des points de vue différents, avec un peu de math (de la géométrie, des équations, c'est bô
), de la physique (l'espace-temps est vraisemblablement encore en construction) et des expériences de pensée (aucune idée si les expériences proposées sont réalisables). Ma foi, que les partisans de l'un ou de l'autre camps proposent des contre-arguments à l'autre camps, j'espère qu'on y répondrad'ailleurs je me lance:
Citation :
Dans le cas du modèle de Lorentz, l'accélération centrifuge a une drôle d'écriture: vRw (doc p12, fin de page), on s'attendait plus à du v².
Dans le cas du modèle de Lorentz, l'accélération centrifuge a une drôle d'écriture: vRw (doc p12, fin de page), on s'attendait plus à du v².
oué ben il s'agit de décrire l'accélération centrifuge dans l'univers observable, il pourrait être tout à fait naturel de 'projeter' v sur Rw...
v et Rw étant de même ordre de grandeur, on peut toutefois se demander si, de vRw ou de v², lequel est prédominent. Est-ce à dire que les satellites, plus rapides que les avions, ont un décalage plus important dans le sens de rotation de la Terre que dans le sens opposé? On peut mesurer l'effet depuis le sol, ou faut-il faire revenir des satellites comme pour les avions?
en fait, il s'agit de savoir quelle équation, entre p11 et p12, est exacte, laquelle est tirée de l'autre, en fait laquelle est une approximation de l'autre, et du coup il faut plutôt chercher aux ordres supérieurs pour discriminer... l'expérience de Haffle&Keating a-t-elle été répétée dans l'espace? Au moins dans un sens, mais dans l'autre?
Encore un sujet à ouvrir...
msg du 08-04-25 à 11:29:
Citation :
Entendons-nous bien: si les photons sont émis sur le quai, ils reviendront (via des miroirs aux extrémités du quai) au milieu. S'ils sont émis dans le train, ils reviendront (via des miroirs aux extrémités du train) au milieu du train. A priori le milieu du train n'a aucun rapport avec le milieu du quai, mais l'expérience devrait être faite pour savoir s'ils peuvent coïncider. A priori les calculs disent que c'est impossible, mais avec le modèle de Lorentz, ça devrait être possible
Entendons-nous bien: si les photons sont émis sur le quai, ils reviendront (via des miroirs aux extrémités du quai) au milieu. S'ils sont émis dans le train, ils reviendront (via des miroirs aux extrémités du train) au milieu du train. A priori le milieu du train n'a aucun rapport avec le milieu du quai, mais l'expérience devrait être faite pour savoir s'ils peuvent coïncider. A priori les calculs disent que c'est impossible, mais avec le modèle de Lorentz, ça devrait être possible
je me relis, je trouve que je ne suis pas clair
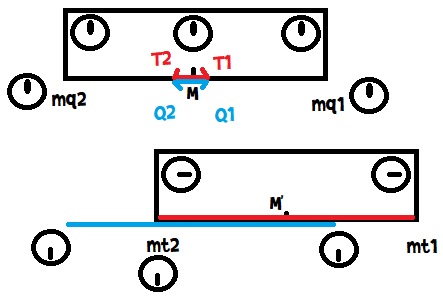
Déjà il faut comparer ce qui est comparable: considérons les photons Q1 et Q2 partant du milieu M du quai (1 pour dire qu'il va dans le sens du mouvement du train), et T1, T2 du milieu du train. Ces deux milieux coïncident quand les photons sont émis
Si on oublie un moment les miroirs du train, ces 4photons, se déplaçant tous à la même vitesse, vont rebondir sur les miroirs du quai (mq1 et mq2) et revenir en M en même temps
Maintenant considérons les miroirs mt1 et mt2 du train, pour que T1 et T2 arrivent en même temps en M' (tout comme mt1 et mt2, le milieu du train se déplace pendant le trajet des photons), il faudrait que, vu du quai, T1 rebondisse sur mt1 se trouvant après mq1 (sur le trajet de T1) et que T2 rebondisse sur mt2 se trouvant avant mq2 (sur le trajet de T2, dans la direction opposée de T1, donc)
Donc voici la conclusion, puisque les Q et T voyagent ensemble, dans le référentiel du quai:
1) sans mt1,2, les T1,2 rebondissent en même temps sur mq1,2
2) avec mt1,2, les T1,2 ne le peuvent plus car l'un doit se trouver au delà de mq1, l'autre avant mq2
De là, on peut parler d'un problème de synchronicité, qu'on liera au fait que ces évènements sont regardés, dans le modèle d'Einstein, depuis un point de vue unique (là où se trouve l'unique horloge du quai ou celle du train). Ici on veut clarifier la situation en plaçant des horloges synchrones un peu partout
Se déplaçant à la même vitesse, les horloges du train à l'avant et à l'arrière du train, synchrones, subissent le même décalage: si l'on arrête le train, elles afficheront la même horaire, différente de celle du quai certes, mais la même
lorsque T2 et Q2 arrivent en mt2, depuis le train on peut regarder l'horloge située à cet endroit sur le quai, cet horaire indique bien que Q2 n'a pas encore atteint mq2. On peut aussi noter l'horaire à l'arrière du train, et on sait qu'à cette horaire, à l'autre bout du train, T1 se trouve en mt1, mais alors il y a contradiction puisque Q1, qui est supposé se balader avec T1, aurait alors déjà dépassé mq1, d'autant que l'horaire notée sur le quai à cet endroit sur le quai, la même que précédemment, indique que Q1 ne peut se trouver au delà de mq1 (Q2 n'a pas encore atteint mq2)
Si on reste sur les hypothèses d'Einstein, à savoir que T 1,2 se baladent avec Q1,2, on arrive donc nécessairement à une contradiction. Après mûre réflexion, je me dis qu'il y a un biais: les horloges du train mesure un écoulement du temps pour ce qui est statique dans le train. Dès lors que nous nous déplaçons dans le train, nous devons considérer un écoulement différent, surtout si l'on compare un mouvement dans le sens de celui du train avec le même dans le sens opposé (les vitesses ne sont pas additives, surtout, comme le schéma le propose, quand la vitesse du train est proche de c). Donc il faudrait considérer un écoulement différent du temps pour T2 et T1 (en un certain sens, un photon voit le temps s'écouler, son trajet perso n'est donc pas instantané). Et si l'on tient à ce que les horloges indiquent le même décalage à l'avant et l'arrière du train, il faut alors considérer que l'espace (ou plutôt la géométrie) traversé par T1 et T2 ne sont pas les mêmes, de sorte que T1 et T2 se déplacent, en apparence donc, à c dans le train. Les effets sur le temps et l'espace seraient donc concomitants et antagonistes de sorte que la vitesse de la lumière reste constante dans le train, c'est le modèle de Lorentz. Pour T1, l'écoulement du temps correspond à celui d'une horloge que l'on percevrait en regardant (à la jumelle et dans la direction de mouvement, "en aval") une horloge immobile placée sur les rails (on verrait un temps accéléré, les photons de l'horloge mettent moins de temps pour parvenir au train), et pour T2, on regarderait une horloge placée "en amont" (on verrait un temps ralenti, les photons de l'horloge mettent plus de temps pour parvenir au train)
On ne peut donc se contenter de deux horloges synchrones dans le train, celles-ci n'étant calées que sur l'horloge en aval depuis un référentiel statique dans le train (aucun mouvement dans le train). Puisque depuis l'extrémité 1 du train on ne peut recevoir de photons émis dans le train se déplaçant dans le sens opposé au mouvement du train, on peut placer à côté de H1 une seule horloge calée sur le temps mesuré avec l'horloge en aval, plus rapide que H1, et idem, une horloge à côté de H2 calée sur l'horloge en amont, plus lente que H2. Le temps indiqué par H1 peut alors être corrigé pour donner le temps indiqué sur le quai au même endroit. Idem pour H2
Reprenons: à l'arrêt du train, on constera bien que H1 et H2 sont synchrones, elles présentent le même décalage avec les horloges du quai. Elles doivent cependant recevoir une correction pour indiquer que les photons qui parcourent le train de l'avant vers l'arrière, comme T2, càd dans la direction opposée au mouvement, croisent les photons émis par l'horloge en amont. Idem, les photons comme T1 croisent les photons émis par l'horloge en aval. Et j'espère que tout le monde comprend que la brochette de photons croisés par T1 ne sera pas la même que celle de T2: T1 est plus gourmand. Si personne ne me devance, et si la modération ne finit pas par bloquer ce fil de discussion (je squatte un peu là), je ferais un calcul de cette correction, afin de finaliser la clarté désirée. A la fin, le miracle doit s'opérer: T et Q voyagent en même temps, ils rebondissent en même temps sur leurs miroirs respectifs et les H, sans correction, indiquent la même horaire. Et la contradiction constatée auparavant n'est alors plus qu'un paradoxe
sur le schéma je fais arriver T et Q en même temps sur leur miroirs respectifs, c'est abusif. Si on veut coller un minimum au modèle d'Einstein, il faut que les miroirs du train soient distants de la longueur du train en mouvement (la longueur à l'arrêt corrigé du facteur de Lorentz). Cela ne change rien à la logique utilisée, le déplacement du train (en o(v)) n'a rien à voir avec la variation de sa longueur (en o(1-v²)). Que ce soit du point de vue des horloges du quai ou du train, l'avant, le milieu et l'arrière du train coïncident avec trois points sur le quai, et les horloges démarrent alors toutes en même temps
Dans ce schéma tout est plat, il faut imaginer un plan fixe (le quai) avec des horloges synchrones tout le long du quai, et un autre plan, en mouvement, avec deux horloges synchrones distantes de la longueur du train, ce plan glissant sur le premier (quand on regarde sur le quai depuis le train, on regarde une horloge qui colle à la fenêtre, et on a le nez sur la fenêtre), on cherche à se distinguer du modèle d'Einstein où l'horloge est unique sur le quai, ici il faut les horloges en aval et amont ainsi que des horloges qui collent au fenêtre, on a à la fois un point de vue local et distant (le global étant alors estimable via une interpolation entre le local et le distant). Si je donne l'impression de complexifier les choses, c'est surtout parceque le modèle d'Einstein est trop simple, mais ce n'est qu'une vue de l'esprit: Lorentz à l'ordre 1, c'est du Einstein à l'ordre 2 (les horloges H doivent être corrigée) parcequ'à l'ordre 1, on obtient une contradiction
Citation :
il faut que les miroirs du train soient distants de la longueur du train en mouvement
il faut que les miroirs du train soient distants de la longueur du train en mouvement
arf, on a beau se relire.. Il fallait bien entendu lire
Citation :
il faut que les miroirs du quai soient distants de la longueur du train en mouvement
il faut que les miroirs du quai soient distants de la longueur du train en mouvement
les 3points sur le quai sont marqués lors du passage du train. La simultanéité de ce marquage peut amener une difficulté technique, qui peut être corrigé avec des photos synchrones depuis le quai
Bon, puisque l'on mesure la longueur du train avec des photons, qui peuvent aller dans le sens du mouvement comme dans l'autre, on doit s'attendre à deux mesures, l'une indiquant une dilatation, l'autre une compression, dixit le modèle de Lorentz. Et ici, vu que les photons partent du milieu du train en sens opposé, on doit s'attendre à une moitié de train dilatée, l'autre compressée. Vu l'additivité non linéaire des vitesses, on peut s'attendre à ce que l'un ne compense pas l'autre et que, globalement (si on fait faire un AR à un photon dans le train), la longueur du train ne soit pas pour autant conservée, que l'on retrouve le fait que le train est rétréci (je fais un parallèle avec un trajet dans un vaisseau quittant la Terre: à l'aller le temps observé sur Terre à la jumelle depuis la lucarne arrière est ralenti, mais c'est surtout au retour que l'on voit (par le 'parebrise') le temps en accéléré (cf cette histoire de brochette de photons, cette fois-ci attrapée par le vaisseau) et, à haute vitesse, ce temps est prépondérant par rapport au premier (on retrouve le résultat d'Einstein, globalement, sur un AR, le temps ralentit dans le vaisseau relativement à celui s'écoulant sur Terre))
Je fais donc le pari que la variation calculée (mesurée par un photon AR) de la longueur du train sera plus prononcé par la compression que par la dilatation. Bref
bonjour,
Citation :
je me relis, je trouve que je ne suis pas clair
je me relis, je trouve que je ne suis pas clair
Il serait temps de vous en rendre compte!
Vos posts sont quasi incompréhensibles!
C'est pourquoi je vous conseille par ex. les cours en ligne d'Etienne Parizot (sur YT) ou de Richard Taillet pour acquérir les bases et revenir ensuite, si nécessaire, poser des questions précises concernant la physique moderne.
Bonjour,
Il n'y aucune contradiction :
Référentiel du train
0 Émission x=0 ; t=0
1 Réception miroir 1 ;
2 Réception miroir 2 ;
3 Réception au milieu du train ;
Référentiel du quai
0 x'=0 ; t'=0
1 ;
2 ;
3 ;
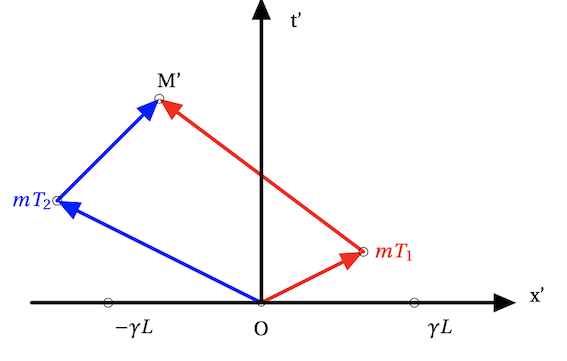
Photon 1 : départ en 0, rebond en , arrivée en
, soit une distance de
Photon 2 : départ en 0, rebond en , arrivée en
, soit une distance de
Il parcourt tous les deux la même distance et tous les deux à la vitesse c.
Votre problème réside dans :
- "le modèle d'Einstein, depuis un point de vue unique" ; NON, il y a une infinité d'horloge et celle que l'on prend en compte c'est celle où l'on se trouve.
- "les horloges du train à l'avant et à l'arrière du train subissent le même décalage" ; NON, je vous ai déjà donné des liens.
krinn: Vos posts sont quasi incompréhensibles!
qu'est-ce qui est incompréhensible, le fait que les deux cercles de rayon L et R ne coïncident pas? on est d'accord
Sinon, je t'invite à intervenir là où je pourrais me planter, les premiers messages ne sont pas des pavés comme à la fin...
Citation :
Il n'y aucune contradiction
Il n'y aucune contradiction
Vu que personne ne veut s'attaquer à mon raisonnement, il faudrait que je m'attaque à celui que l'on me sort. Ce n'est pas très symétrique tout ça...
Et bien au boulot!
Référentiel du train OK: t1 est le temps marqué par H1, t2 par H2, t3 par une horloge au milieu du train. Elles sont regardées par des personnes statiques dans le train, le nez dessus
Référentiel du quai: quelles sont les horloges indiquant t1', t2', t3', par qui sont-elles regardées, à quelle distance, vitesse relative?
Bonjour,
Citation :
quelles sont les horloges indiquant t1', t2', t3', par qui sont-elles regardées, à quelle distance, vitesse relative?
quelles sont les horloges indiquant t1', t2', t3', par qui sont-elles regardées, à quelle distance, vitesse relative?
L'horloge indiquant t'3 est celle qui se situe juste en face du milieu du train lorsque les photons arrivent, la personne qui regarde est juste en face du milieu du train en x'3.
Pour t'2 remplacer "du milieu du train lorsque les photons arrivent" par l'extrémité du train lorsque le photon se réfléchit sur le miroir 2.
La vitesse relative est v. Remarque : je m'aperçois que mon train va dans le sens inverse du votre, mais comme c'est algébrique...
Citation :
Pour t'2 remplacer "du milieu du train lorsque les photons arrivent" par l'extrémité du train lorsque le photon se réfléchit sur le miroir 2.
Pour t'2 remplacer "du milieu du train lorsque les photons arrivent" par l'extrémité du train lorsque le photon se réfléchit sur le miroir 2.
donc j'imagine qu'il y a quelqu'un qui note l'horloge du quai (t2') qui se trouve à l'endroit M2 où le photon T2 arrive sur mt2 (c'est mal dit mais comme les plans glissent l'un sur l'autre cet endroit du quai se confond avec l'arrière du train où se trouve mt2), et une autre personne qui note l'horloge du quai (t1') qui se trouve à l'endroit M1 où le photon T1 arrive sur le miroir mt1
Et ces horloges afficheraient une horaire différente.
A t1' (<t2'), on peut savoir où se trouve l'arrière du train (on note où se trouve l'arrière du train lorsqu'elle se pointe devant une horloge indiquant t1', et on marque le quai M2", c'est la fête aux primes). M2' n'est donc pas au même endroit que M2". M2' se trouve plus loin sur le quai, lorsque l'arrière du train se pointe devant une horloge du quai indiquant t2'
c'est bien ça?
C'est bien cela.
On trouve x'(M2")= et x'(M1)-x'(M2")=
, on retrouve bien que la longueur du train a été contracté.
Citation :
M2' n'est donc pas au même endroit que M2". M2' se trouve plus loin sur le quai, lorsque l'arrière du train se pointe devant une horloge du quai indiquant t2'
M2' n'est donc pas au même endroit que M2". M2' se trouve plus loin sur le quai, lorsque l'arrière du train se pointe devant une horloge du quai indiquant t2'
il fallait bien sûr lire M2 au lieu des M2'. Du coup on peut noter M2' au lieu de M2". Ce ne serait pas drôle si on ne se trompait pas un peu...
Je ne comprends pas pourquoi tu prends M2' au lieu de M2. Les photons du trains, on les a envoyés pour mesurer la longueur du train depuis le quai, on ne doit retenir que M2 et M1, c'est le but de l'expérience, non? Quourpoi retiendrait-on M2' si T2 ne l'a pas encore atteint?
D'autre part, ton gamma fait une valse par rapport au message du 22-04-25 à 14:27... pourrais-tu corriger?
Sinon, je ne comprends pas que l'on puisse marquer M1 avant M2, il me parait nécessaire que, puisque T1 va dans le sens de mouvement du train, il mette plus de temps (dans le référentiel du quai) pour atteindre M1 que T2 pour atteindre M2. C'est parceque tu as pris le train à l'envers? Pourrais-tu réécrire ton message du 22-04-25 à 14:27 en tenant compte de mon schéma stp?
bon, heureusement qu'on prend l'habitude de lire entre les lignes
Référentiel du train
0 Émission x=0 ; t=0
1 Réception miroir 1
2 Réception miroir 2
3 Réception au milieu du train
Référentiel du quai
0 x'=0 ; t'=0
1
2
3
Dans ce sens là, ça marche mieux, t1>t2. mes messages du 22-04-25 à 17:30 et 22-04-25 à 20:16, restent donc inchangé, ma question reste la même:
pourquoi considérer M2'(t1') et non M2(t2'), l'endroit où le photon T2 atteint mt2?
Citation :
Je ne comprends pas pourquoi tu prends M2' au lieu de M2.
Je ne comprends pas pourquoi tu prends M2' au lieu de M2.
J'ai simplement répondu à la question : "savoir où se trouve l'arrière du train..."
De quelle valse parlez-vous ?
Citation :
C'est parce que tu as pris le train à l'envers ?
C'est parce que tu as pris le train à l'envers ?
Message de 16h30 : " Remarque : je m'aperçois que mon train va dans le sens inverse du votre, mais comme c'est algébrique..."
Citation :
pourquoi considérer M2'(t1') et non M2(t2'), l'endroit où le photon T2 atteint mt2?
pourquoi considérer M2'(t1') et non M2(t2'), l'endroit où le photon T2 atteint mt2?
Parce que "savoir où se trouve l'arrière du train...", c'est M2' et M2(t'2) est déjà donné.
Bonjour,
Je vous ai donné des liens textuels, krinn vous a donné des liens video, si vous préférez du papier :
L'univers en perspective: Relativité restreinte. Jean-Marie Vigoureux.
et non
Et finalement, en changeant le sens du train, c'est M1'(t2') qu'il faut considérer, et non M2'(t1') et x'(M1') =
Les pinceaux se démêlent.. 
Citation :
De quelle valse parlez-vous ?
De quelle valse parlez-vous ?
le gamma passe de multiple à diviseur
(tu peux aller directement au dernier paragraphe, je suis OK avec les calculs, sauf le dernier (x'(M2"), c'est à dire x'(M1') dorénavant), du message 22-04-25 à 19:16, qui me parait complètement faux, je trouve x'(M1') =
Citation :
savoir où se trouve l'arrière du train...
savoir où se trouve l'arrière du train...
et bien entre les photons
Pour estimer la longueur du train depuis le quai:
entre celle où l'on prendrait la longueur
Il en existe même une troisième: on envoie, depuis le quai, après son passage, deux photons sur le train, l'un rebondissant sur l'arrière du train, l'autre sur l'avant. Le temps entre leur retour donne une longueur apparente de (4vL/c)/2. Pas de gamma pour celle-ci
Ou encore on attend que le train passe (chrono entre le passage de l'avant et celui de l'arrière), on mesure à priori le temps t=2L/v, parceque t.v = 2L
On prend laquelle?
[facultatif, je voulais voir où les calculs menaient]
Si on prend les résultats du message précédent, entre
Réciproquement, par symétrie, si on place deux miroirs sur le quai en M2"(t1') et M1(t1'), et une double source de photon au milieu (M'), on peut donc tirer une paire de photon T1' et T2' à la date
[/facultatif]
La définition de la distance est assez essentielle, on pourrait chercher à s'entendre. Mais ma question n'est pas là, je suis d'accord avec les calculs, et ceux-ci indiquent que t_1' et t_2' sont différents, on s'en doutait parceque T1 met plus de temps pour atteindre mq1 que T2 et mq2
Dans le train, les photons arrivent à la même horaire T à l'avant et l'arrière
Si on poste sur le quai quelqu'un à l'avant et un autre à l'arrière à l'instant où T1&2 atteignent leur miroir respectif, qu'espèrent-ils voir s'afficher sur leur horloge? La même horaire non, différente de T, mais la même non? Que le train se déplace vers la droite ou la gauche, l'effet temporel de la vitesse est identique, les deux horloges se décalent de la même vitesse d'horloge, les deux bonhommes devraient constater le même décalage, non? Quand le train s'arrête, elles indiqueront bien la même horaire, décalée
Le problème est le même depuis le début :
Citation :
Si on poste sur le quai quelqu'un à l'avant et un autre à l'arrière à l'instant où T1&2 atteignent leur miroir respectif, qu'espèrent-ils voir s'afficher sur leur horloge? La même horaire non,
Si on poste sur le quai quelqu'un à l'avant et un autre à l'arrière à l'instant où T1&2 atteignent leur miroir respectif, qu'espèrent-ils voir s'afficher sur leur horloge? La même horaire non,
Encore une fois non, ce qui est simultané dans le train ne l'est pas pour le quai. Mais l'explication en cinq lignes dans le cadre d'un forum me parait difficile, je vous ai donné des liens, krinn aussi, il y aussi le bouquin ...
Le γ qui passe de numérateur à dénominateur est normal, il résulte des calculs et est cohérent avec la contraction des longueurs.
Citation :
Le γ qui passe de numérateur à dénominateur est normal, il résulte des calculs et est cohérent avec la contraction des longueurs.
Le γ qui passe de numérateur à dénominateur est normal, il résulte des calculs et est cohérent avec la contraction des longueurs.
tu veux dire que
Le second membre est obtenu avec tes résultats du msg 22-04-25 à 14:27
Citation :
Encore une fois non, ce qui est simultané dans le train ne l'est pas pour le quai.
Encore une fois non, ce qui est simultané dans le train ne l'est pas pour le quai.
on est d'accord, les calculs l'indiquent bien
mais ce n'est pas ma question
Citation :
Mais l'explication en cinq lignes dans le cadre d'un forum me parait difficile
Mais l'explication en cinq lignes dans le cadre d'un forum me parait difficile
Effectivement, j'ai du écrire un pavé pour comprendre, du moins proposer une solution. Même si je ne vais pas lire un bouquin de plusieurs centaines de pages (j'ai coché 'Master' pour ce message, j'ai déjà plus qu'un aperçu de la relativité), pourrais-tu m'indiquer à quel endroit j'aurais une réponse précise? J'ai peur que la contradiction ne soit pas évoquée, même sous une forme apparente, j'imagine que le décalage est introduit quelque part, les calculs ailleurs, mais pas de confrontation entre les deux
De mon point de vue, le pavé est plus court que le bouquin. Bon, j'y ai promis quelques calculs...
Citation :
mais ce n'est pas ma question
mais ce n'est pas ma question
euh ça n'a rien à faire là. Ou alors disons que la simultanéité apparente observée, lorsque le train s'arrête, à l'avant et l'arrière, bien que décalée avec le quai, ne peut expliquer effectivement le décalage entre
La question de la simultanéité "dans le train mais pas pour le quai" me parait être une description (les calculs), pas une explication. Avec cet adage, on pourrait être en droit de s'attendre à ce que les horloges du train restent décalées entre elles (telle une trace signifiant la non simultanéité avec Q1&2) dans le train après s'être arrêté. Et malheureusement, pas de trace!
Et finalement, puisque la question de la longueur d'un mobile semble trouver une réponse un peu arbitraire (cf la partie 'sautable' du msg 23-04-25 à 08:42, il semble que la question se pose beaucoup moins quand les photons font un trajet AR, la longueur MM' ou OM' permettant permettant de connaître le temps de vol des photons, et donc la double longueur du train), j'estime qu'il faut regarder ce qui se passe à la moitié du trajet des photons. Cette démarche suit celle qui permet de détailler le comportement du temps lors de l'aller puis lors du retour, par un vaisseau qui part&revient (tu l'as déjà eu sous les yeux, la Terre envoie des bips régulièrement, il suffit de les compter lors de l'aller, puis lors du retour, pour déterminer le temps qui s'écoule sur Terre), le modèle d'Einstein considère l'AR, il ne fait pas le détail de l'aller et du retour (vitesse v, même facteur de Lorentz, même rapport au temps). Si on se contente d'un AR c'est facile donc, mais si on passe par l'A puis le R, on doit aussi obtenir une physique (avec un photon sonde qui va vers l'amont, un autre vers l'aval, cf l'histoire de la brochette dans le pavé du 22-04-25 à 12:22, il faut une mesure à l'arrêt, en somme pour synchroniser les horloges du train, et une autre en mouvement, et on peut même affiner avec un arrêt 'absolu', sans dipôle cosmologique, et un mouvement composite) qui doit permettre les observations à la fin de l'AR
Annuler
connectez vous