Inscription / Connexion Nouveau Sujet
Graphique sur l’accélération
Bonjour,
Voici l'énoncé de l'exercice : « Le graphique position-temps d'un objet se déplaçant en ligne droite est représenté ci-dessous (P est la position, t est le temps). L'allure du graphique (position-temps) représenté :
1. est compatible avec le graphique 1
2. est compatible avec le graphique 2
3. est compatible avec le graphique 3
4. n'est compatible avec aucun des trois graphiques
Le correctif me donne la réponse B mais je n'arrive pas à comprendre comment c'est possible. Ça signifie que l'accélération est constante et négative, et pourtant la position du mobile augmente. Pourriez-vous m'expliquer ce que j'oublie de prendre en compte ou ce que je comprends mal ? Merci d'avance,
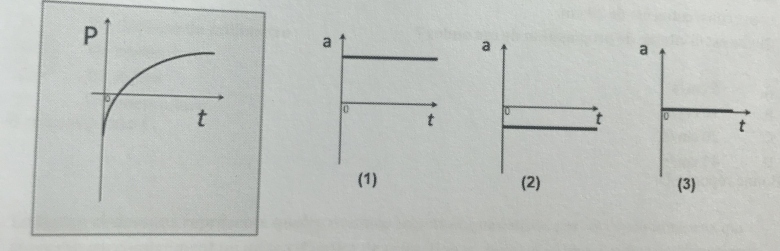
Si a(t) = - ao
alors v(t) = -ao.t + vo
et x(t) = -1/2.ao.t² + vo.t + xo --> c'est bien l'allure d'une parabole inversée, ce qui est logique avec le constat physique.
En effet, si l'accélération est négative, on aura un mouvement rectiligne décéléré, la vitesse va donc diminuer au fil du temps (ce qu'on constate en voyant la pente de la tangente à la courbe position diminuer au cours du temps).
Puis, lorsque la vitesse devient nulle, la position se stabilise (pente de la tangente à la courbe nulle).

Merci pour vos explications, j'ai enfin compris. Mon problème était que je partais du principe qu'à la base, le mobile était au repos et qu'il démarrait donc avec une vitesse nulle ce qui ne coïncidait donc pas avec une accélération négative. Je n'avais pas pris en compte le fait qu'il avait une certaine vitesse initiale. Encore merci !

 !
!
