Inscription / Connexion Nouveau Sujet
Freinage et sécurité routière
Bonsoir, voilà le sujet:
Lorsqu'un automobiliste décide de s'arrêter, on considère que le véhicule, animé d'une vitesse V, parcourt une distance pendant
une durée correspondant à la durée de réaction du conducteur sans appuyer sur le frein, puis une distance
pendant une durée
correspondant à la durée effective du freinage. La distance d'arrêt est alors la somme de
et
Le mouvement du véhicule, de masse M et de centre d'inertie G, est étudié dans un référentiel terrestre supposé galiléen. Il est
assimilé à un mouvement de translation rectiligne de direction horizontale.
1. Distance de réaction
Pendant la durée on peut considérer que la somme des forces qui agissent sur le véhicule est nulle.
a) Déterminer la nature du mouvement du véhicule. Justifier la réponse.
b) Calculer, à partir des valeurs du tableau, le rapport . La distance
est-elle proportionnelle à la vitesse ?
c) En déduire la durée exprimée en secondes, utilisée pour déterminer toutes les valeurs
du tableau.
2. Distance de freinage.
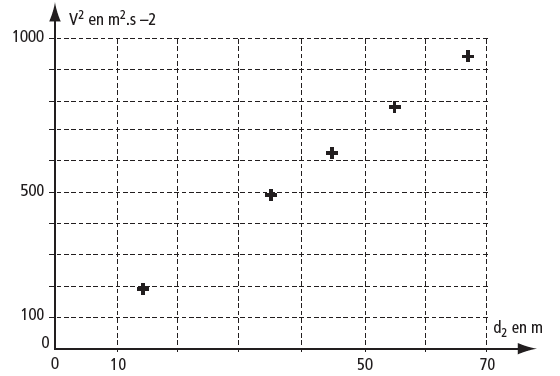
À partir des données du tableau, on a obtenu la représentation graphique ci-dessous.
a) Déterminer graphiquement la valeur de la vitesse, exprimée en , correspondant à la distance
b) Calculer le coefficient directeur de la droite.
c) La force de freinage est assimilée à une force constante de direction horizontale, de sens opposé au vecteur vitesse et devaleur F.
- Représenter, sur un schéma, les forces appliquées au véhicule.
- Soit V la valeur de la vitesse au début du freinage. Établir la relation entre et
- Établir la relation : , dans laquelle k représente le coefficient directeur calculé au b). En déduire la valeur numérique de F.
Donnée: M =
RÉPONSES:
1.
a) D'après le principe d'inertie, dans le référentiel galiléen, tout corps qui n'est soumis à aucune force est soit immobile soit en mouvement rectiligne uniforme. Ici il est en mouvement donc mouvement rectiligne?
b) Il faut que je convertisse d'abord le km en m, non? De toutes façons le rapport est constant car on trouve la même valeur à chaque fois.
c) celle qu'on trouve à la b)?
2.
a) 66km/h
b) 14,4 (à partir de la relation )
c) Je ne sais pas
Merci de m'aider!
Tout le reste est bon je dirais.
Pour la 2c) :
PFD de Newton:
M a = -F et on suppose que F est constante
=> v(t) = -F*t/M + V
avec v(t=0_instantdefreinage) = V.
la distance parcourue après début du freinage en fonction du temps est :
d[/sub](t) = -F*t2/(2M) + V*t
Le temps du freinage 
t[sub]2 s'obtient par la condition
immédiate que v(t2) = 0
soit t2 = VM/F
et donc d2 = d[/sub](t[sub]2)
soit d2 = V2M/(2F) attention j'ai fais le calcul très vite donc vérifie toi-même si c'est bon. En tout cas çà à l'air cohérent avec la conservation de l'énergie.
En plus cette dernière relation te montre que :
F = V²M/(2d2) soit la forme demandée F = kM/2 où k = V2/d2 qui si je me souviens bien est le coefficient directeur de la courbe que tu as déjà calculé.
J'ai du mal à comprendre tout ça. Dans mon cours je ne vois rien sur ça donc je ne comprends pas comment t'arrives à déduire ça
(les forces sont bien: poids, frottements et réaction normale?)
Le poids et la réaction du support se compensent. Heureusement sinon la voiture aurait un mouvement verticale.
Tu n'as pas eu de cours sur la loi de Newton et la résolution de cette équation du mouvement pour une force constante ?
C'est-à-dire? Pour réaliser le schéma j'aimerais faire le bilan des forces, ce que j'ai mis est bon ou non?
En fait lorsque je fais un devoir je regarde la séquence sur laquelle je dois travailler + la séquence précédente et je ne trouve rien dur les relations que t'as écrites.
Dans tous les cas, la question te demande de faire un schéma donc oui les forces que tu as donné sont bonnes.
Après pour la résolution tu as deux choix, soit résoudre l'équation de Newton soit te servir de la conservation de l'énergie mécanique. Peut-être est-ce que tu as vu récemment en cours ? (travail d'une force, énergie cinétique)
Je suppose qu'il faut utiliser le TEC et déduire une formule à partir de là.
On a bien dans la formule mais pas
donc comment faire?
Salut,
je m'incruste étant donné que je bosse sur le même devoir ^^, j'en suis à la même question et je pense avoir trouver ... Mais le truc c'est que je ne sais pas si on peu utilisé la donnée de la masse pour cette partie de la question mais je suis partie du fait que oui:
Je vous passe les explicatifs du genre 2 des 3 forces s'annulent et tout ça...
0.5mVB2 - 0.5mVA2=
WAB(Fext)
0.5mVB2 - 0.5mVA2= WAB(F)
0.5mVB2 - 0.5mVA2= mgLsin
0.5 
830 V4 - 0.5 830 V2 = 830 9.8 d2
415V4-415V2=8134d2
Mais bon sur ce coup la je ne suis pas du tout sur de moi =/
donc comment faire
Tu dois absolument savoir la chose suivante si tu as eu un cours sur énergie cinétique, force et travail :
La variation d'énergie cinétique le long d'une trajectoire est égale au travail de la résultante des forces extérieures sur cette trajectoire.
Toutes les forces perpendiculaires au mouvement ne travaillent pas (ici poids et réaction du sol). La seule force qui travaille c'est la force de frottement qui modélise le freinage et que l'on considère comme constante et bien sur opposé au mouvement de la voiture.
La voiture à une vitesse initial V, le but c'est de trouver sur quelle distance d2 la force de freinage doit travailler pour arrêter la voiture (v=0) c'est-à-dire dissiper son énergie cinétique.
Application du TEC :
Ec = Ec_final - Ec_initial = 0 - 1/2mV2 = - F * d2
d'où la relation trouvée entre d2 et V2
Annuler
connectez vous