Inscription / Connexion Nouveau Sujet
Forces s'exercant sur un solide dur!!
voila je ne sais pas comment faire merci de votre aide. Je vous pose mon problème:
Une poutre homogène AB est appuyée sur un mur vertical et repose en B sur le sol. On admet que le contact sur le mur est sans frottement et que le frottement du sol sur l'extrémité B est suffisant pour empêcher tout glissement.
Données: Masse de la poutre m=10kg; AB=5m, OB=3m g=10N/kg.
Déterminer les réactions RA et RB exercées par les murs en A et B sur la poutre.
PS: Pour déterminer la direction de RB on se servira des conditions d'équilibre(forces concourantes)
Voila merci d'avance de votre aide
Bonjour quand même...
Puisqu'il n'y a pas de frottement en A quelle est la direction de RA ?
Que vaut la distance OA ?
Considère les moments au point B :
. ceux des forces qui s'exercent en B sont nuls
. il y a le moment du poids
. il y a le moment de RA
Tu peux donc calculer RA
La somme des forces qui s'exercent sur la poutre est nulle (puisque la poutre est immobile)
Quelles sont donc les composantes horizontale et verticale de RB ?
Quelle est la norme de RB ?

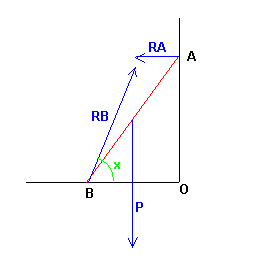
Projection sur une axe vertical:
P = RB.sin(X)
Projection sur une axe horizontal:
RA = RB.cos(X)
Moment autour de B:
P*(OB/2) - RA * OA = 0
...
Sauf erreur on arrive à:
RA = 37,5 N
RB = 96,6 N
X = 69,4°
-----
Sauf distraction. 
Bonjour( excuser moi de cette impolitesse!!)
merci J-P j'avais fait le meme dessin que toi mais que veut tu dire en mettant "moment autour de B"? peut tu m'expliquer comment on trouve les résultats merci beaucoup!
La projection des forces sur 2 axes non //, permet d'avoir 2 équations liant les 3 inconnues RA, RB et X.
Il manque donc une équation pour pouvoir déterminer les inconnues.
On peut trouver cette 3ème équation en exprimant que la poutre ne tourne pas autour d'un point quelconque.
Ici, ce point a été choisi en B car c'est assez simple dans ce cas.
Comme la poutre est fixe, elle ne tourne pas autour du point B.
Donc si on fait la somme des moments (des couples) des forces par rapport à B, on doit trouver 0.
Ceci permet d'avoir une 3ème équation liant les 3 inconnues RA, RB et X
Il y a plus de détail sur la notion de moment dans ce lien: ![]()
Lire le chapitre: "Moment par rapport à un point".

Bonsoir
j'ai touvé comme toi sauf pour RB ou j'ai trouvé qu'il valait 106.7 N. Peux tu détailer le passage au niveau des axes s'il te plait
Merci de ton aide w
Bonjour kefran et bonjour J-P 
kefran >> Pour ma part je confirme une norme de égale à 106,8 N
Puisque = 37,5 N les deux composantes de
au point B sont :
. une composante horizontale égale et opposée à , donc d'intensité 37,5 N
. une composante verticale égale et opposée à , donc d'intensité 100 N
L'angle entre et l'horizontale vaut bien
X = Arctg(100 / 37,5) = tan-1 (100 / 37,5)  69,4°
69,4°

Voila ce qui arrive quand on calcule dans sa tête. 
P = RB.sin(X)
Projection sur une axe horizontal:
RA = RB.cos(X)
Moment autour de B:
P*(OB/2) - RA * OA = 0
P*(OB/2) - RA * OA = 0
10*10*1,5 - RA*4 = 0
RA = 37,5 N
100 = RB.sin(X)
37,5 = RB.cos(X)
--> tg(x) = 100/37,5
X = 69,4°
P = RB.sin(X)
100 = RB.sin(69,4°)
RB = 106,8 N
-----
Autrement:
Moment autour de B:
P*(OB/2) - RA * OA = 0
10*10*1,5 - RA*4 = 0
RA = 37,5 N
Pythagore: P² + RA² = RB²
100² + 37,5² = RB²
RB = 106,8 N
P = RB.sin(X)
100 = 106,8.sin(X)
X = 69,4°
-----
Sauf nouvelle distraction. 


