Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Forces s'excercant sur un solide

Posté par
crayon 22-10-09 à 21:55

Bonjour,

J'ai un devoir maison en Physiques et j'ai essayé de le résoudre mais je n'y arrive pas.

Voici l'énoncé :

Un déménageur pousse un meuble, de masse m = 120 kg, posé sur une moquette. La force F (il y a une flèche sur le F) qu'il excerce est horizontale, de valeur 600 N. Le meuble ne bouge pas.

a) Représenter sur un schéma la force F ( il y a une flèche sur le F) excercée par le déménageur ainsi que le poids du meuble.
Echelle proposée : 1 cm 600 N.

b) A quelle autre force le meuble est-il soumis ?

c) Quelle est la relation qui existe entre ces trois forces ? Justifier.

Données : Intensité du champ de pesanteur : g = 10 N.kg-1


Merci beaucoup d'avance

Cordialement

Posté par
Marc35re : Forces s'excercant sur un solide 23-10-09 à 12:52

Bonjour,
a) Je suppose que tu sais faire ...
b) S'il y a une force horizontale de 600 N et que le meuble ne bouge pas, c'est qu'il existe une troisième force : la force de frottement.
S'il n'y avait pas de frottement, la réaction du support \vec{R} serait verticale et \vec{P}\,+\,\vec{R}\,=\,\vec{0}
c) Qu'en penses-tu ?

Posté par
crayonre : Forces s'excercant sur un solide 23-10-09 à 22:14

Bonjour,

Merci d'avoir répondu

Alors, tout d'abord,

- pour la question a), il faut donc représenter le poids du meuble qui va être une flèche qui aura pour origne le centre de gravité du meuble et qui sera vers le bas ( vers la Terre ). Mais, sachant que l'échelle est de 1 cm 600 N, combien mesurera alors la flèche représentant le poids ?
Je pense que cela a un rapporrt avec l'intensité du champ de pesanteur qui g = 10 N.kg-1 mais je ne vois comment m'y prendre . . .
Pour la représentation de la force F, il faut juste faire une flèche horizontale de 1 cm non ?

- pour la question c) , il y a donc trois forces : le poids, la force F , et la force de frottement.
Par contre, je vois pas la relation entre ces trois forces, à part peut-être que la force F et la force de frottement se compensent puisque le meuble ne bouge pas ?

Posté par
Marc35re : Forces s'excercant sur un solide 24-10-09 à 13:52

Le poids du meuble est : 120 x 10 = 1200 N
1 cm 600 N donc pour le poids du meuble ==> 2 cm
Pour la force F qui fait 600 N ==> 1 cm   bien sûr

Les forces sont comme sur le schéma ci-dessous.
On a :  \vec{P}\,+\,\vec{F}\,+\,\vec{f}\,=\,\vec{0}
parce que le meuble ne bouge pas (première loi de Newton).
\vec{f}  est la force de frottement qui se décompose en une composante verticale  \vec{R} qui est égale et opposée au poids et une composante  \vec{T} qui est égale et opposée à la force   \vec{F}
\vec{P}\,+\,\vec{R}\,=\,\vec{0}
\vec{F}\,+\,\vec{T}\,=\,\vec{0}

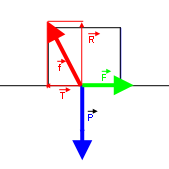
Forces s\'excercant sur un solide

Posté par
crayonre : Forces s'excercant sur un solide 24-10-09 à 17:43

Merci beaucoup, je comprends vraiment mieux maintenant avec le schéma !

Cependant, je ne comprends certains éléments : je ne vois pas d'où vient la force T, et je voudrais quelques éclaircissements sur la valeur graphique de la force de frottements f et savoir si elle est égale à la réaction R .

Posté par
Marc35re : Forces s'excercant sur un solide 24-10-09 à 18:20

Quand il n'y a pas de frottement, la réaction du support \vec{R} est égale à  -\vec{P}. Si on applique une force \vec{F} , le meuble glisse sans problème.
S'il y a des frottements, la réaction du support n'est plus verticale. Elle est inclinée et d'autant plus que les frottements sont plus importants. Elle peut se décomposer en une force verticale \vec{R}  qui est la réaction du support sans frottement et une composante horizontale  \vec{T}  qui s'oppose au déplacement.
On a :
\vec{R}\,=\,-\vec{P}
\vec{T}\,=\,-\vec{F}
ou
\vec{f}\,=\,-\big(\vec{P}\,+\,\vec{F}\big)

La force \vec{f} a donc une norme égale à :
||\vec{f}||\,=\,sqrt{1200^2\,+\,600^2\,}\,=\,sqrt{(2\times600)^2\,+\,600^2\,}\,=\,sqrt{600^2\times(4+1)\,}
||\vec{f}||\,=\,600\,sqrt{5}

J'espère que c'est plus clair ...

Posté par
Marc35re : Forces s'excercant sur un solide 24-10-09 à 18:27

||\vec{f}||\,=\,600\,sqrt{5}\,\,\bold{N}   bien sûr

Posté par
crayonre : Forces s'excercant sur un solide 25-10-09 à 17:27

Encore merci d'avoir répondu !

Oui, c'est certes plus clair mais le calcul de la norme, je ne le comprends pas ....

D'où viennnent la racine et le carré ? et le " (4+1) " ?

Posté par
Marc35re : Forces s'excercant sur un solide 25-10-09 à 18:24

On a:
\vec{P}\,+\,\vec{F}\,+\,\vec{f}\,=\,\vec{0 }
Ou :
\vec{f}\,=\,-\big(\vec{P}\,+\,\vec{F}\big)
Donc :
||\vec{f}||\,=\,||\vec{P}\,+\,\vec{F}||
Les vecteurs  \vec{P}  et  \vec{F}   sont perpendiculaires. Donc, P et F forment un triangle rectangle dont l'hypoténuse est f. Donc, par application du théorème de Pythagore :
||\vec{f}||\,=\,sqrt{P^2+F^2}
Sachant que P = 1200 et F = 600, le calcul est dans le message précédent.
Le (4+1) provient de la mise en facteur de 6002
||\vec{f}||\,=\,sqrt{1200^2\,+\,600^2\,}\,=\,sqrt{(2\times600)^2\,+\,600^2\,}\,=\,sqrt{(4\times600^2)\,+\,600^2\,}\,=\,sqrt{600^2\times(4+1)\,}

J'espère que c'est limpide

Posté par
crayonre : Forces s'excercant sur un solide 26-10-09 à 23:05

Ah oui, je vois . . . il fallait donc penser au théorème de Pythagore avec le triangle rectangle !!!

Bon, bah, je pense que je vais pouvoir commencer la rédaction du devoir !

En tout cas, encore merci beaucoup pour cette grande aide et tous ces petits éclaircissements !!!


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !