Inscription / Connexion Nouveau Sujet
forces electrostatiques
salut j'ai un probleme sur cet exercice
deux charges ponctuelles q1 et q2 sont placées dans le vide respectivement en A ET B on pose AB=10cm
trouver un point de la droite AB ou le vecteur champ electrique resultant est nul on envisagera deux cas;
a) q1 et q2 ont la meme signe
b) q1 est positif ET Q2 est negatif
on donne |q1|=6000nc et |q2|=5000nc
j'ai vu la correction mais on m'a dit que la resultante en dehors de A mais du cote B (c'est cette partie que je ne comprend pas)
Bonjour,
La charge de A est plus forte que la charge de B
Donc pour une égalité des intensités des champs créés par ces deux charges il faudra se trouver plus loin de A que de B
Si les charges ont même signe (question a) il faut se trouver entre A et B
Si les charges ont des signes différents, il faut se trouver à l'extérieur du segment AB ; mais pour être plus près de B il faut être du côté de B

deux charges ponctuelles q1 et q2 sont placées dans le vide respectivement en A ET B on pose AB=10cm
trouver un point de la droite AB ou le vecteur champ electrique resultant est nul on envisagera deux cas;
a) q1 et q2 ont la meme signe
b) q1 est positif ET Q2 est negatif
on donne |q1|=6000nc et |q2|=5000nc
Bonjour,
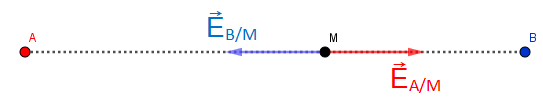
En A une charge (par exemple) positive de 6000 nC crée au point M le champ
En B une charge demême signe de 5000 nC crée au point M le champ
Le champ résultant en A est nul ce qui implique que les vecteurs et
sont opposés et ont donc la même norme : EA/M = EB/M
AM = x ( inconnue à trouver)
AB = 10 cm
Odbugt1 merci d'avoir répondu
Oui j'ai fais MB=x et AM=d-x avec d =10cm donc on aura k*qa/(d-x)2=k*qb/(x)2 mais après j'ai une équation du second degré ce que je trouve est fausse a mon avis
C'est pas mal du tout !
Tu as seulement une erreur de calcul entre la 2e ligne (exacte) et la 3e
J'ai obtenu : x² / (d-x)² = k qB / k qA
et en simplifiant :
x² / (d-x)² = qB/qA = 5/6
Je te laisse continuer ......
Je trouve x2/(d-x)2=6/5
 x2-1,2x+0,06=0 et je trouve un x=5cm (sûrement quand les deux sont positifs) et un x=115cm ( quand l'un négatif l'autre positif)
x2-1,2x+0,06=0 et je trouve un x=5cm (sûrement quand les deux sont positifs) et un x=115cm ( quand l'un négatif l'autre positif)
C'est bon???
Ne trouvant pas le même résultat que toi je reprends mon calcul :
qA = 6000 nC
qB = 5000 nC
d = 0,10m
Je pose comme toi MB = x ( j'avais proposé dans mon post de 21-04-18 à 19:55 MA = x mais bien entendu
MB = x est tout aussi valable.)
Le point M est nécessairement situé entre A et B et plus proche de B que de A .
Je m'attends à trouver x < 0,05m donc x<5cm
k.qB / x² = k.qA / (d-x)²
Je simplifie par k :
qB / x² = qA / (d-x)²
qB / qA = x² / (d-x)²
qB = 5000 nC qA = 6000 nC
qB / qA = 5000 / 6000 = 5/6
x² / (d-x)²= 5/6
5 (d-x)² = 6x²
x² + 10d.x - 5d² = 0
x² + x - 0,05 = 0
2 Racines : x1 = 0,0477m ≈ 4,8cm
et x2 = -1,0477 m ( à rejeter car M entre A et B )
On trouve bien que comme prévu x< 5cm
Le cas ou les charges sont de signes contraires doit faire l'objet d'une autre analyse.
Le point M n'étant plus entre A et B, mais du côté de B
Si on pose encore MB = x on aura simultanément MA = d + x
Mais une autre question pour le calcul du vecteur champ le vecteur unitaire me pose vraiment problème ou bien c'est toujours égale à 1?? Pourrais-tu m'eclairer là-dessus


