Inscription / Connexion Nouveau Sujet
force gravitationnelle
Bonjour, ceci n'est pas un exercice noté ni à rendre mais je vous remercie de m'aider 
Soit une fusée de masse mF allant sur la Lune de masse mL décollant de la Terre de masse mT.
On note F la force exercée par la fusée sur la Lune et H la force exercée par la fusée sur la Terre.
On note également que la distance Terre Lune est d.
Nous cherchons à savoir à quelle distance d G sera égal à F.
Ainsi d'après la loi d'attraction gravitationnelle de Newton on a:
F = G ( mL * mF )/ d²
et
H = G ( mT * mF )/ d²
Ainsi je fait en sorte que d soit isolé ce qui donne:
d = 
G*mL*mF
et
d = G*mT*mF
sachant que mT vaut 5,972.1024 kg et que mL vaut 7,36.1022 kg
l'équation devient d = G*mT*mF / G*mL*mF
En simplifiant je pensais écrire que d = mT / mL mais au final le résultat est 9 km et je ne trouve pas ça cohérent sachant que la distance d = 384 400 km.. Je pense qu'il y a une erreur dès le début de mon raisonnement Merci d'avance pour votre aide
Tu n'as pas, à mon avis, compris ce qu'on te demande (qui est d'ailleurs confus de la manière où c'est écrit, il manque des mots).
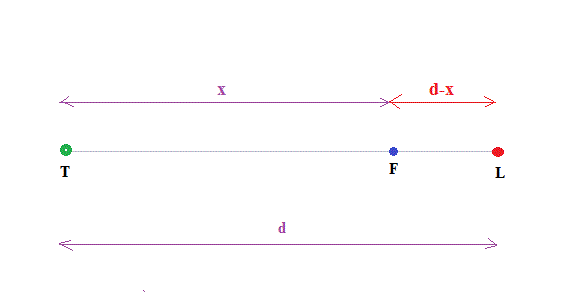
F = G * mL * mF/(d-x)²
H = G * mT * mF/x²
F = G si : G * mL * mF/(d-x)² = G * mT * mF/x²
mL /(d-x)² = mT /x²
On connaît mT, mL et d ---> on peut calculer x qui est la distance entre la fusée et la Terre pour avoir |F| = |G|
Sauf distraction.
Zut, dans mon message précédent, lire :
F = H si : G * mL * mF/(d-x)² = G * mT * mF/x²
et aussi :
... on peut calculer x qui est la distance entre la fusée et la Terre pour avoir |F| = |H|
Annuler
connectez vous