Bonjour (base de toute politesse),

Tu n'es pas un nouveau membre, tu dois donc connaître les règles :

extrait de la FAQ du forum :

Q01 - Que dois-je faire avant de poster une question ?

Plusieurs choses sont à faire avant d'envisager de poser une question sur le forum.

Tout d'abord, réellement chercher à résoudre seul votre problème. En effet, le but du forum n'est pas de faire les exercices à votre place.

Cherchez également si votre question n'a pas déjà été posée sur le forum. Pour cela vous pouvez utiliser le moteur de recherche (en panne pour le moment) ou le net en tapant quelques mots clés, par exemple, le début de votre énoncé.

Vous pouvez aussi parcourir le forum en choisissant une classe spécifique (de la sixième au supérieur) dans la page de choix du forum. Vous trouverez certainement un exercice déjà posté et corrigé qui ressemblera fortement au vôtre.

Enfin, vous pouvez également consulter les fiches du site se rapportant à votre chapitre. Parfois une simple relecture de celles-ci vous permettra de vous rappeler d'une définition, d'une propriété, d'une condition d'application d'une loi (données, hypothèses, ...), d'une méthode oubliée, etc.

Somme toute, n'envoyez pas le sujet d'un exercice sans montrer que vous y avez travaillé sérieusement.

Bonjour,

Pour t'aider efficacement à répondre à la question 3, il faut s'appuyer sur la figure demandée à la question 1.
On attend donc tout particulièrement que tu postes cette figure.

Bonjour,
Alors, Désolé c'est la première fois que je pose une question dans ce forums.
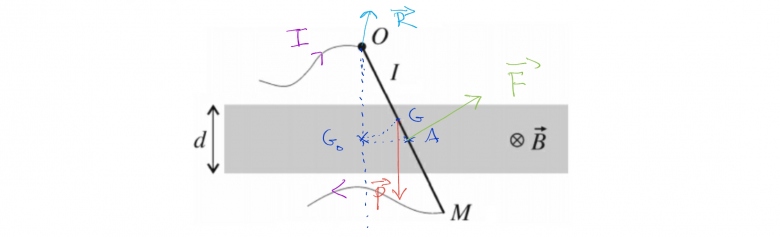
la figure est la suivante:
j'ai représenté les forces et le sens de courant.
pour la troisième question je me trouve avec une équation du 3eme ordre.

La condition d'équilibre: M(P)+M(F)+M(R)=0
Avec :
M(R)=0
M(P)=-mg OG sin(θ)=-mg OM sin(θ)/2
et M(F)=F.d' avec d'=OM/2cos(θ) et F= IdB/cos(θ)
d'où
sin(θ).cos(θ)^2=IdB/mg

Je pense que compte tenu que " d " est relativement petit devant OM on peut considérer que le point d'application de la force de Laplace est pratiquement confondu avec le centre de gravité du conducteur.

Merci beaucoup, pour votre réponse.
Si on fait cette approximation, peut-on faire aussi l'approximation des angles petits: sin θ=θ et cos θ=1?

Bonjour à vous deux,

@badrov : pourrais-tu mettre à jour ton profil et préciser que tu es en première (d'après ce sujet créé), ce sera une information pour les membres qui t'aident et pour adapter leur discours

extrait de la FAQ du forum :

Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau topic ?

Oui, indiquer son niveau (dans son profil) et celui du problème est obligatoire lorsqu'on pose une question.

Un correcteur pourra ainsi facilement juger s'il est en mesure de vous aider ou non. En l'absence de cette précision, aussi bien sur votre profil que sur le forum dans lequel le sujet est publié, il risque moins de vous indiquer une méthode que vous n'avez pas encore vue en classe, etc.

De même, si vous êtes élèves dans un pays francophone, vous pouvez consulter les équivalences des systèmes de niveaux scolaires afin de choisir le niveau de la classe française correspondant à votre classe. Cela permet au correcteur d'intégrer le fait que votre niveau scolaire ne correspond pas forcément à celui stipulé dans les programmes français en vigueur.

Merci, infiniment.