Le probleme c'est que c'est un schema, d'habitude je met les questions

Je pars de ce pas faire une explication de mon probleme ^^

Bonjour!

En effet, il serait génial que tu mettes ce qu'il faut

Merci d'avance

Oui ça veut dire quoi tu crois les formules?

F n'est pas passé de gauche à droite, je vois pas les indices mais les deux expressions semblent identiques et simplement séparées par une virgule...


Pour comprendre le schéma il faut avoir appréhendé l'explication dans son intégralité. Qu'as-tu retenu? Si je te demande une définition courte et simple de la force de Coriolis, il en ressort quoi?

Tout d'abord merci de ton aide

En fait pour moi la force de Coriolis c'est 2 pussance vecteur de la vitesse du point M.
=La Vitesse Angulaire * Vecteur Zo qui est pour moi egale à 1 quand la direction est Sud Nord et moins 1 pour Nord Sud

Concernant les expressions ou j'ai dit qu'elle sont passé de gauche à droite je crois que je n'ai strictement rien compris en fait je crois le texte qui dit que les accélérations d'entrainement et de Coriolis disparaissent mais la compensation je ne comprend pas ...

Et si tu oubliais les calculs pour te focaliser sur la définition. Une fois que tu l'auras comprise, tu pourras parler de calculs tu crois pas?

Okay Chef ^^

Alors de tete pour moi la force de coriolis est une principe d'Inertie qui "permet de faire dévier" un corps, Cette déviation va vers la droite dans l'hémisphère Nord alors que c'est l'inverse dans l'hémisphère Sud. Plus on s'éloigne de l'Equateur plus cette  force est importante

Ca reste tres vague dans ma tete  ...

Bon je vais tenter une déf complète:
C'est une force qui s'applique aux objets en mouvement placés sur un objet en mouvement de rotation (comme la Terre). La force de Coriolis est due à l'inertie de l'objet et à la rotation de la Terre autour de son axe. Ainsi, cette force dévie les trajectoires des objets vers la droite dans l'hémisphère Nord, vers la gauche dans l'hémisphère Sud pour un observateur regardant la Terre de l'espace. Cette force est nulle à l'équateur et maximale aux pôles, elle ne se fait sentir que sur les objets en mouvement. A cause de cette force, on observe dans les cours d'eau de l'hémisphère nord une érosion plus importante de la rive droite que de la rive gauche. Cette force de Coriolis a un effet sur le déplacement de l'atmosphère et de l'hydrosphère. Les différences de températures entre l'équateur et les pôles font qu'il existe un gradient de pression dirigé du nord vers le sud, les vents auraient donc une direction nord-sud dans l'hémisphère nord. La force de Coriolis leur donne une direction est-ouest. Qd il existe une haute pression dans l'hémisphère nord, les vents tournent dans le sens des aiguilles d'une montre formant un tourbillon caractéristique.

Tu peux faire le rapprochement avec les circulations atosphériques et océaniques...

Ca te va? Tu piges?

Pardon je rédigais pour avoir la meilleure définition possible ce qui fait que je n'avis pas vu ta réponse.

Tu avais de bonnes idées, tu avais saisi le principal...

Je suppose que tu avais déjà trouvé ce site mais bon:

[url]
http://www.ac-nantes.fr:8080/peda/disc/scphy/dochtml/foucault/cyclones.htm[/url] ça illustre les rapprochements que je te demande de faire





et je pense la réponse à ta question de vecteurs même si je pense l'avoir explicité sur la fin de l'explication:


Ce sont les sites les plus interessants que j'ai pu trouver sur la mise en relation Coriolis/cyclones.

Ah un lien est mal passé:

Ok j'ai tout bien compris ^^

Maintenant grâce a quel relation mathematique on prouve que l'objet est dévié vers la droite dans l'Hemisphere Nord et inversement ?

En fait pour mon TPE j'aimerais bien pouvé ça parce que si j'arrive a comprendre et ressortir les explications mathematiques du dessus les profs vont aimé je pense ^^

Ne t'embete pas à repondre je vais voir les sites que tu m'as dit ^^

Dsl du bouble post

Ce sont les relations où tu as mis la mention "déjà je comprend moyen le passage de gauche à droite"...

Pas grave, ça m'arrive souvent de faire du flood quand j'oublie des trucs ou qu'on répond en même temps...

Ceci aussi l'explique:

Et bien? Tu es rassasié ou t'es parti goûter peut-être...?

Merci beaucoup pour ces liens je suis en train d'essayer de comprendre le plus long, le reste c'est Ok

En fait c'est les fomrules ou j'ai du mal par ex


Rappel de la loi de composition des vitesses

En mécanique, la loi de composition des vitesses qu'on utilise est assez intuitive. Imaginons comme dans la première partie le passager d'un train marchant à 5 km/h dans un train roulant à 150 km/h. Une vache regardant passer le train : elle dira que le passager avance à 155 km/h. Exprimons ceci mathématiquement. Considérons deux référentiels R et R', R' se déplaçant à la vitesse U par rapport à R, supposé fixe. Imaginons une particule P se déplaçant à la vitesse V' par rapport à R'. Alors la loi de composition des vitesses donne V la vitesse de P par rapport à R :

V = U + V'

Dans le cas où R' est en rotation par rapport à R autour d'un axe z, à la vitesse angulaire : Ω = Ω.ez

U = Ω x r

V = Ω x r + V'

La c'est ok


On obtient :


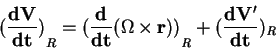
*** image placée sur l'***

LA je ne comprends plus pourtant j'ai bien lus et je comprend le principe.

En fait c'est sur la meme chose que je bute, parce que sur mon lien c'est quand je parlais du passage de gauche a droite que je ne comprenais plus et sur ton lien a la fin de la demonstration on arrive à la meme equation

Merci d'avance

Non non je suis toujours present mais j'ai bien epluché tes liens :p

lol juste quand je t'écris

Tu ne comprends pas quoi dans tous les cas? Les mises en équations ou bien les transformations?

Ok c'est bien que tu épluches les liens, ça prouve que ça t'interesse, pourtant je pensais que t'avais déjà dû les trouver...

Je ne comprend pas le passe de
U = Ω x r

V = Ω x r + V'  

à la formule avec les (dV/dt)R...

D'ou sorte les d ?

Je pense que quand j'aurais compris cette ligne ça sera bon ^^

Je n'en avais pas trouvé 2 mais les autres a vrai dire je l'ai avait lus sans plus j'ai surtout essayer de comprendre le lien que je t'ai passé au debut

Ok, concernant ta formule c'est vrai que les d sont étranges. Je ne comprend pas vraiment d'où ils sortent non plus... Peut-être s'agit-il de coeff mais dans ce as ils ne servent à rien.
D'ailleurs on pourrait logiquement les supprimer à mon sens...

Désolé du temps de réponse j'aidais qqn d'autre sur les transfets thermiques...

transferts thermiques* pardon

Ok c'est po rav je vais faire sans parce que apres je comprends le principe
Merci beaucoup de ton aide ^^
(Enfin si qqn peut m'expliquer d'ou viennent les d je veux bien

Je vais essayer de te trouver un physicien dans le coin

Mici ^^

Pas de quoi pour ma part, ce fut un plaisir de te venir en aide, j'ai toujours été très interessée par ce type de forces...

Bonne journée et bonne continuation Bon courage pour la suite

Adiù

Je vais essayer de te dégoter Coll ou un autre bon physicien

Okay merci ^^

Peut-être que ça prendra un peu de temps par contre, car il n'y en a pas bcp de connectés en ce moment et les autres ont bcp de boulôt...

Tu auras la réponse ce soir au plus tard je pense...

T'inquiete pas j'ai encore plein de choses a faire lol

Merci beaucoup

Pas de quoi, moi aussi j'ai du travail mais vu que ça se passe sur des docs internet

J'ai râté Coll désolé, tu n'auras la réponse que demain s'il est là (et je pense sincérement que ce sera le cas)... Heureusement ça n'avait pas l'air urgent...

Okay pas de pb ^^

Bonjour à tous les deux

Je n'ai pas beaucoup de temps aujourd'hui et je ne vais répondre que partiellement.

Je vais essayer d'expliquer un peu le post du 19 à 15 h 58

La deuxième loi de Newton n'est valable que dans un référentiel galiléen. Très souvent on fait l'approximation que la Terre en est un. Mais on ne peut pas faire cette approximation en météorologie car la force de Coriolis bien que très faible est du même ordre de grandeur que la force qui met en mouvement les masses d'air... donc il faut la prendre en compte !

Si tu admets la formule qui donne l'accélération de Coriolis
alors la suite n'est pas trop compliquée.

La relation fondamentale de la dynamique (deuxième loi de Newton) n'est valable que dans un référentilel galiléen (par exemple, approximativement, un référentiel géocentrique) :



Mais

Si bien que pour décrire dans le référentiel terrestre (qui n'est pas galiléen) le mouvement caractérisé par son accélération

On va ajouter à la force des forces "fictives" :



Par identification tu retrouves :



et



Donc la force de Coriolis est de même direction mais de sens opposé à l'accélération de Coriolis.

Quel est le sens de l'accélération de Coriolis dans l'hémisphère Nord ?

Regarde le produit vectoriel qui définit l'accélération de Coriolis. Dans l'hémisphère Nord le vecteur rotation terrestre sort du sol et pointe (plus ou moins selon la latitude) vers le haut ; donc le produit vectoriel donne toujours un sens vers la gauche de la vitesse relative.

Conséquence : la force de Coriolis qui est de sens opposé à l'accélération donne toujours un sens à droite de la vitesse relative (dans l'hémisphère Nord)

Vive la réponse partielle

T'assures trop là bravo

Vraiment merci bcp Coll d'avoir pris le temps de répondre à ce problème malgré tout le boulot que tu as

Un petit topo sur les forces "fictives" ou forces "d'inertie" :

Si on dit qu'une force résulte directement d'une interaction fondamentale (gravitationnelle ou électromagnétique ou forte ou faible) alors les forces "fictives" n'existent pas.

Si on dit qu'une force est un outil inventé par les physiciens pour décrire les phénomènes observés, alors les forces "fictives" peuvent être un outil commode.

Je m'amuse à tenir un pendule (comme le professeur Tournesol...) dans un train qui est à l'arrêt (situation 1) puis qui accélère avec une accélération constante (situation 2) et enfin qui roule d'un mouvement rectiligne uniforme (situation 3) :



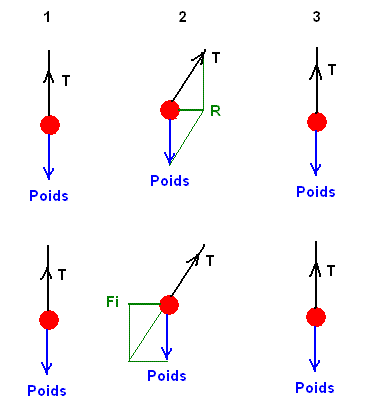
Première ligne : l'interprétation du physicien qui se place dans un référentiel galiléen (un référentiel terrestre pourrait, ici, convenir) :
1 : le poids est équilibré par la tension T du fil. Somme nulle. Pendule immobile et vertical (la direction du fil est à peu près celle du centre de la "Terre" - le "à peu près" vient justement de ce que la Terre tourne et que le référentiel terrestre n'est pas un référentiel galiléen, mais oublions cela)

2 : le point d'attache du pendule (ma main) est soumis à une accélération vers la droite : le train accélère vers la droite. Je dis que pour que la boule du pendule soit accélérée elle aussi vers la droite il faut que la résultante des forces auxquelles elle est soumise soit dirigée dans le sens du mouvement.



Conclusion : le fil est incliné dans la direction opposée au mouvement du train ; la résultante du poids et de la tension du fil est bien vers l'avant. La boule est accélérée vers l'avant.

3 : le train roule à vitesse uniforme et avec une trajectoire rectiligne : il n'y a plus d'accélération. Le pendule est comme à l'arrêt. Galilée disait à peu près : le mouvement rectiligne uniforme est "comme rien".
______________

Deuxième ligne : l'interprétation du physicien qui est dans un référentiel non galiléen (le train qui accélére) et qui veut interpréter les phénomènes dans ce référentiel.

1 : interprétation inchangée.

2 : pendant que le train accélère je constate que le pendule se dirige à l'opposé du mouvement du train et (l'accélération étant supposée constante) qu'il reste immobile dans cette position inclinée.
Je veux absolument utiliser la première loi de Newton dans ce référentiel non galiléen : je dis que puisque le pendule est immobile c'est que la somme des forces qui s'appliquent sur lui a une résultante nulle. Je connais le poids, force verticale ; je connais la tension du fil dont je sais que sa direction est celle du fil et son sens de la boule vers ma main ; je conclus qu'il doit exister une force F_i que j'appelle force d'inertie, dirigée à l'opposé de l'accélération du train.

3: interprétation inchangée
______________

Les forces "centrifuge" et "de Coriolis" sont de la même manière des forces "fictives" ; elles ne résultent pas d'une interaction fondamentale mais elles sont introduites dans les référentiels non galiléens pour permettre de continuer d'y appliquer les lois de Newton qui ne s'y appliquent normalement pas.

Ce petit exemple montre aussi comment la force fictive est de sens opposé à celui de l'accélération pour laquelle elle est introduite. Si l'accélération du train et donc de ma main est vers la droite, la force fictive est de sens opposé, vers la gauche.



D'accord ?

Et moi qui comptais te demander un peu plus tard ce qu'était une force "fictive" (j'avais déjà vu J-P en parler dans un autre topic et ça m'intriguait énormément je l'avoue), là je suis servie.

Là je pense que Bnj a tout ce qu'il faut

Mais quelque chose me chiffone toujours: pourquoi "fictives"?

Je n'ai pas vraiment le temps d'aller voir tous les liens que tu postes (et je le regrette, car tu as sûrement fait des choix pertinents).

Force fictive : elle ne représente pas une interaction

Force fictive : elle est introduite pour représenter une accélération dans un référentiel non galiléen. Dans un référentiel galiléen cette accélération n'est pas nécessaire pour décrire le mouvement et donc... on n'y introduit pas cette force fictive.

Va faire un tour ce week-end dans l'aire de jeux la plus proche de chez toi avec deux ami(e)s

Assieds-toi sur le tourniquet immobile. Tes deux ami(e)s sont de part et d'autre du tourniquet (diamétralement opposé(e)s) et se lancent une balle, par dessus ta tête et le tourniquet.

En bonne physicienne, tu regardes le mouvement de la balle et "modélise" par des forces et des équations cette cinématique et cette dynamique : quel mouvement, quelle trajectoire et quelle(s) force(s) nécessaire(s) pour en rendre compte.

Aussi longtemps que le tourniquet est immobile tu peux considérer être, comme tes ami(e)s, dans un référentiel galiléen. Il te suffit d'imaginer que les forces en présence sont le poids, la résistance de l'air pour un ballon de faible masse volumique (la poussée d'Archimède si vraiment tu veux ne rien oublier)... et, aussi bien pour toi que pour tes ami(e)s, cet ensemble de forces suffit à décrire la belle parabole (s'il n'y a que le poids) que décrit la balle.

Mets maintenant le tourniquet en rotation. Tu n'es plus dans un référentiel galiléen. Rien ne change pour tes ami(e)s qui continuent de se lancer la balle. Mais, oh surprise, voilà que pour toi la trajectoire est courbée (vers la droite si tu fais tourner le tourniquet dans le sens inverse de celui des aiguilles d'une montre - l'hémisphère Nord - ) : tu ne peux plus expliquer ce mouvement avec les seules accélérations de tout à l'heure qui suffisent toujours à tes ami(e)s. Il te faut introduire une accélération pour expliquer cette courbure (c'est la cinématique). Et comme tu es physicienne et que tu veux continuer à utiliser les lois de Newton, tu vas dire : s'il y a une accélération nouvelle c'est qu'il y a une force nouvelle (c'est la dynamique).

Qui a raison ? Toi ou tes ami(e)s ? Tout le monde a raison.

Conclusion(s) :
. les lois de Newton sont valables dans un référentiel galiléen
. dans un référentiel non galiléen on peut continuer à utiliser les lois de Newton à la condition d'introduire des "forces" qui ne résultent pas d'une interaction fondamentale mais de la nature non galiléenne du référentiel.

Houla faudrait que je prenne l'habitude de relire avant de poster...

lire "exactement" et "aux morts"

Adiù

Ouuuh je suis que de passage sur l'ordi mais vraiment un grand merci Coll

Je me penche dessus ce soir mais normalment je vais pas avoir trop de mal a comprendre

N'oublie pas de faire aussi tourner le tourniquet dans le sens des aiguilles d'une montre (hémisphère Sud) pour voir la trajectoire déviée vers la gauche...

Coll--->Oui sinon ça va être le contraire
Merci encore

Bnj--->En effet, les explications de Coll sont toujours très claires, tu devrais y arriver sans problèmes...

Adiù

bonjour à tous,

Coll>>

excellent ! je me demandait justement hier ce qu'était cette fameuse force d'inertie, tes explication sont vraiment super comme toujours

Amandine et Bnj>>

A ok, évidement moi sortie des notations habituelles

"évidemment"* pardon