Inscription / Connexion Nouveau Sujet
Exercices sur les satellites
Bonjour, j'ai ici un devoir de physique qui m'embrouille un peu.
Donc, pour la question 1, je sais la faire, pour la question 2, je sais que:
R^3= (T^2xG.mT)/4pi^2
Pour T^2 j'aurais besoin d'aide ainsi que pour les autres questions
merci d'avance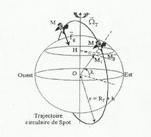
** énoncé effacé ; image laissée **
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
Voici le sujet:
Spot (de masse m) est placé sur orbite circulaire qui effectue 369 révolutions en 26 jours (dans le referentiel géocentrique)
La terre de masse MT et de Rayon RT est assimilée à une sphère homogène.
donnée: soit go intensité de pesanteur terrestre au sol (go=G.MT/RT^2= 9,8m.s-2), RT= 6370 km, MT= 5,98 10 exposant 24 et G=6,67 10exposant-11
1) calculer l'altitude h puis la vitesse de spot. Pourquoi son orbite est elle appelée orbite polaire?
Donc je sais que (RT+ h)^3= (T^2xG.mT)/4pi^2 et la période de révolution est: (26/369)x 24X3600= 6087,8
d'ou (RT+h)^3= 3,744e20
donc (RT+h)= racine cubique de 3,744e20
6370+h= 7207399,8
h= pas possible car trop grand
je suis bloqué pour la vitesse et l'altitude
2) le satellite est à la verticale d'un point Mzero de la terre à la latitude lambda (y). Après 71 révolutions, il est à la verticale d'un autre point Mun de la terre.Montrez que les points Mzero et Mun sont sur un meme parallèle. callculer la distance d MzeroMun en fonction de lambda.
Données: T=7.3 10exposant 5 rad.s-1 (vitesse angulaire de la terre autour de l'axe des poles)
Bonjour,
Merci pour l'énoncé.
Peux-tu ré-écrire toutes les données avec leurs unités ?
Peux-tu ré-écrire toutes tes réponses avec leurs unités ?
En physique un résultat sans son unité ne veut strictement rien dire.
Et ainsi tu trouveras peut-être ton erreur...
J'allais te demander quelle est l'unité de T justement,
Sinon a part çà, j'ai réussi à calculer la vitesse et l'altitude:
vitesse de spot= 7,4km/s-1
altitude= 833km
J'aurais besoin d'aide pour la question 2 et la question: Pourquoi son orbite est elle appelée orbite polaire?
T= 6087,8s
(RT+h)^3= [6.67.10^-11 x 5,98.10^24 x (6087,8)^2] / 4pi^2
on trouve donc (RT+h)^3= 3.744.10^20
RT+h= racine cubique de 3.744.10^20
RT+h= 7207399,8.10^-3 km
6370km + h = 7207399,8.10^-3 km
d'ou h =837,399 (je crois que j'ai confondue le 7 avec le 3)
Pour la vitesse, v^2= (gzero x RT^2)/ (RT+h)
v^2= (9.8x6370.10^3m)/ (6370.10^3+ 837)
v^2= 55173729,41
v= 7427,9 m/s
v= 7,43 kmm/s
Oui,
je trouve h 
837,7 km
et v 7 439 m.s-1 ou 7,44 km.s-1
Attention à l'écriture des unités :
Vitesse en mètres par seconde : m/s ou m.s-1
Vitesse en kilomètres par seconde : km/s ou km.s-1
Quel est le référentiel adapté à l'étude du mouvement du satellite ?
Le satellite se trouve en un point quelconque de son orbite. Où se trouve-t-il après une durée égale à une période ?
Quel est le référentiel adapté à l'étude du mouvement du satellite ?
Référentiel géocentrique?
Le satellite se trouve en un point quelconque de son orbite. Où se trouve-t-il après une durée égale à une période ?
Il se retrouve au meme point.
Je vois pas comment il faut faire pour:
calculer la distance d MzeroMun en fonction de lambda.
Données: T=7.3 10exposant 5 rad.s-1 (vitesse angulaire de la terre autour de l'axe des poles)
Attend!
c'est en 26 jours que le satellite revient au meme point donc,
La période du satellite est égale à la durée nécessaire pour passer de la verticale du point Mzero à la verticale du point Mun, non?
Le référentiel :
Oui, il est préférable de choisir un référentiel géocentrique.
Dans ce référentiel on va choisir ainsi les axes du repère :
Origine du repère en O, centre de la Terre
Axe Oz : selon l'axe de rotation de la Terre. Donc il pointe du côté de l'étoile polaire
Axes Ox et Oy : tous les deux dans le plan de l'équateur terrestre (mais ils ne sont pas liés à la Terre ; ils pointent vers des étoiles très lointaines)
Dans ce référentiel :
La Terre tourne autour de l'axe Oz
Le plan de l'orbite du satellite est immobile
Le satellite se trouve en un point quelconque de son orbite. Où se trouve-t-il après une durée égale à une période ?
Il se retrouve au même point.
Oui, il se retrouve au même point dans le référentiel géocentrique.
Supposons que la droite OM qui joint le centre de la Terre au satellite fasse l'angle
avec le plan Oxy quand il se trouve en ce point quelconque de son orbite, après une durée égale à une période (T 6 087,8 s) cette droite OM fera à nouveau l'angle avec le plan Oxy
Donc :
Si en ce point quelconque de l'orbite le satellite se situe à la verticale d'un point de la Terre dont la latitude vaut
il se trouvera après une période à la verticale d'un autre point de la Terre dont la latitude vaudra à nouveau
Et ainsi après chaque durée d'une période.
Après 71 révolutions, il sera encore à la verticale d'un point de la Terre de latitude
Cependant, pendant une révolution du satellite, la Terre tourne...
Et donc après une révolution du satellite, il se retrouve à la verticale d'un point de même latitude mais d'une autre longitude.
De quel angle la Terre tourne-t-elle (dans le référentiel géocentrique) autour de l'axe Oz pendant la durée d'une révolution du satellite ?
çà a l'air compliqué (j'ai jamais fait le chapitre sur çà), bref:
je sais pas comment répondre à la question 
, la durée de révolution du satellite est bien de 6087 non? et la terre tourne sur elle meme en 24h
1 tour = 2
rad
24 h = 86 400 s
Mais l'énoncé te donne ce qui convient mieux (car ce n'est pas exactement 24 heures dans un référentiel géocentrique, mais un peu moins)
Vitesse angulaire de rotation de la Terre : 
7,3.10-5 rad.s-1
De quel angle (en radian) tourne la Terre pendant une révolution (T 6 087,8 s) du satellite ?
Je crois comprendre:
la terre tourne de 7.3.10-(rad.s-1 or le temps que met une révolution du satellite est de 6087.8
v=d/t donc d= v.t soit 7.3.10-5*6087.8, non ?
Oui.
Il faut faire le produit et ne pas oublier l'unité du résultat.
Tu connaîtras ainsi l'angle dont la Terre a tourné autour de son axe de rotation (l'axe Oz, axe des pôles) quand le satellite a fait une révolution.
________
L'énoncé te demande cet angle de rotation de la Terre quand le satellite a fait 71 révolutions. Que proposes-tu ?
(n'oublie pas qu'un tour vaut 360° ou, avec l'unité proposée par l'énoncé, 2 radians)
donc, je propose:
calculer combien de temps corresponds à 71 révolutions soit 71x6087,8s= 432233s
d'ou d=v.t= 7,3.10-5x432233= 31rad
Oui, mais il ne faut pas arrondir aussi "brutalement" un résultat intermédiaire.
31,553 radians
Cela correspond à 5 tours de la Terre (5 
2 = 10 radians 31,415 93.. radians) plus (environ) 0,137 14 radians
Il reste à calculer la distance (mesurée le long du parallèle, ce qui ne sera pas la distance la plus courte) entre deux points situés à la même latitude et dont les longitudes diffèrent de 0,137 14 radians.
Tu sais calculer la longueur d'un arc de cercle si tu connais le rayon du cercle et l'angle au centre.
Quand on coupe la sphère terrestre par un plan perpendiculaire à l'axe des pôles et passant par les points de latitude on obtient un cercle. Quel est le rayon de ce cercle (en fonction de RT rayon de la Terre et valeur de la latitude) ?
Si je coupe la sphère terrestre (par la pensée ! ) au niveau de l'équateur (latitude = 0°), le disque obtenu aura pour rayon celui de la sphère terrestre, soit RT
Mais si je coupe la même sphère terrestre au niveau d'un pôle (latitude = 90°), j'obtiens un point... un disque de rayon nul !
Le rayon du disque dépend donc de la latitude.
Première étape : que vaut le rayon du cercle pour un point de latitude ? C'est aussi la distance de ce point de latitude à l'axe des pôles ?
que vaut le rayon du cercle pour un point de latitude ?
si la latitude est de 0 degré, le rayon du cercle reste la meme, par contre, si la latitude vaut 70 degrés par exemple, le rayon du nouveau cercle sera la rayon de ce cercle additionné a 70 degré, non?
Si c'est pas çà, çà veut dire que j'ai pas compris cette partie: (le au niveau des poles,) "Mais si je coupe la même sphère terrestre au niveau d'un pôle (latitude = 90°), j'obtiens un point... un disque de rayon nul ! "
Un schéma :
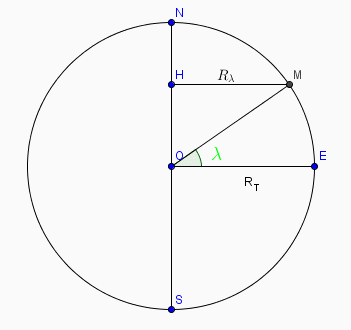
O est le centre de la Terre
N est le pôle Nord
S est le pôle Sud
E est un point de l'équateur
M est un point de latitude
RT est le rayon de la Terre
R est le rayon cherché à la latitude : c'est la distance de H à M
Que vaut R en fonction de RT et de ?
On sait que l'angle de M dans H"M"O est toujours égale à lambda (angle alterne interne)
R en fonction de RT et :
Cos = R
/RT d'ou R= cosH"M"O (31 degré non?) x RT
Oui, à la latitude le rayon du cercle vaut
R = RT cos()
Quand l'angle au centre vaut 2 radians (c'est-à-dire un tour complet) la longueur de l'arc d'un cercle (qui dans ce cas particulier est le périmètre) de rayon R vaut 2 R
Quand l'angle au centre vaut 
radians, la longueur de l'arc d'un cercle de rayon R vaut... R
Donc, je te donne la réponse à la dernière question :
On connaît l'angle au centre : 0,137 14 radian
On connaît la valeur du rayon R à la latitude
Donc deux points de la surface terrestre, situés tous deux à la latitude et séparés par une longitude de 0,137 14 radian sont à une distance, mesurée le long du parallèle (à latitude constante), qui vaut :
d = 0,137 14 RT cos()
d 874 cos() (en km)
On ne connaît pas la latitude (dans ce que tu as posté)
L'énoncé demande de calculer la distance en fonction de
Dans ce que j'ai posté? tu veux dire l'énoncé?
J'ai oublié la question 4) Les caméras spot balaient une surface sur Terre dont une des dimensions est de cent dix sept km, quel est l'interet d'avoir choisi cette période de révolution?
Annuler
connectez vous