Inscription / Connexion Nouveau Sujet
Exercice sur pendule et énergies
Bonjour,
Alors voici l'exercice sur lequel j'ai besoin d'aide :
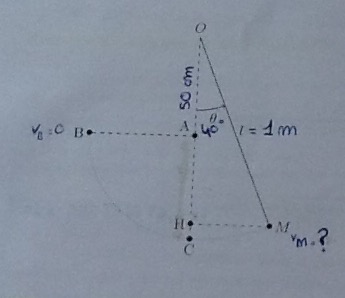
On considère un pendule simple de longueur l = OM = 1 m
On a planté un clou en A tel que OA = l/2
On néglige tous les frottements possibles et on prendra g = 9.81 m.s-2
Voici une photo du schéma de l'exercice, si ça peut aider.
1) On lâche le pendule quand l'angle 
vaut 40°. Avec quelle vitesse doit on le lâcher pour qu'il arrive au point B ?
2) De quel angle doit-on lâcher le pendule sans vitesse pour qu'il arrive au point B ?
Alors, je ne comprends pas comment il faut procéder. En cours nous n'avons vu que la définition des énergies cinétique, de pesanteur et mécanique ainsi que leur formule et nous connaissons la formule v=
2gl(1-cos)
Pourriez vous me dire comment procéder svp ? Merci bien ! 
Salut
Bon alors déjà, petit rappel (j'imagine^^) :
Puisqu'on néglige les forces de frottement, les deux forces qui s'appliquent sur le pendule sont :
- la tension du fil
- le poids
Quelque soit la position du pendule, le vecteur est perpendiculaire à la trajectoire : la seule force qui travaille est donc le poids
, qui est une force conservative.
Il y'a donc conservation de l'énergie mécanique Em, qui vaut :
Em = Ep + Ec
= mgz + 1/2mv²
= mgl(1 - cos) + 1/2mv² (si on pose Ep = 0 pour = 0)
Si tu comprends pas la dernière étape, dis le moi 
L'énergie mécanique étant conservée, tu peux dire qu'entre deux points A et B (appartenant à la trajectoire !) :
Em(A) = Em(B)
mgl(1 - cosA) + 1/2mvA² = mgl(1 - cosB) + 1/2mvB²
Le fait qu'un clou soit présent en A fait que tu dois faire le calcul en deux temps : c'est comme si tu avais deux pendules différents (le premier de longueur l et le second de longueur l/2).
Tu dois donc établir deux relations : une entre B et C, et l'autre entre C et M
Si tu bloques toujours, hésite pas à le dire
Bonsoir,
Alors déjà merci pour l'aide, j'ai déjà compris le principe, maintenant je vais essayer de l'appliquer ! Juste une chose que je n'ai pas comprise, c'est justement ton rappel... Nous n'avons pas abordé ceci en classe, je sais seulement que s'il n'y a pas de frottements l'énergie mécanique se conserve. Est ce que je devrais savoir autre chose ? Et d'ailleurs pour cet exercice, je n'ai pas besoin de savoir le poids du pendule ?
J'essaie de faire l'exercice puis je t'envoie mes résultats si tu veux bien les vérifier.
Encore merci !
Non non excuse-moi, je me suis un peu emballé ! 
En fait je viens de me souvenir que j'avais vu ça en terminale et pas en première... donc je pense avoir fait du hors programme, désolé 
Bon c'est pas grave, ne tiens pas compte de la partie supérieure.
Lis seulement à partir de "Il y'a donc conservation de l'énergie mécanique Em, qui vaut :"
Sinon, est-ce que t'as compris le passage de z à l(1 - cos) ?^^
Et non, tu n'as pas besoin de la masse du pendule, tu comprendras pourquoi
Ce n'est pas grave, ça arrive 😋
Alors oui, j'ai compris, en fait on a zM = OC-OH = l - cos * l = l(1-cos) ! Cest ca ?
J'ai presque fini la première question, je te l'envoie dans un instant, pour savoir si j'ai juste, si tu veux ! 😊
Voici ce que j'ai fait :
On a : l = OM = 1m ; OA= AC = 50cm ; = 40° et g = 9.81 m.s-2
On sait qu'il n'y a pas de frottements donc Em se conserve : Em = Ep + Ec = mgz + 1/2 mv2
On prend Ep(C) = 0 avec z = 0 et on a zM = OC-OH = l - cos* l = l(1-cos) = 0,2 m
Et donc Em = mgl(1-cos)+ 1/2 mv2
On a : Em(M) = mg*(1-cos40)+ 1/2 mvM2 et Em(C) = 1/2 mv2
Pour Em(B), on a l=1/2 m et vB=0 et z= 1/2m donc Em(B)=1/2*mg
Et donc Em(M)=Em(C)=Em(B)
mg*(1-cos40)+ 1/2 mvM2 = 1/2 mv2 = 1/2*mg
(Je te passe la longue partie de l'équation)
Et donc on trouve vM = g-2g(1-cos40) = 2,28 m/s = 8,208 km/h !
Voilà, est ce juste ?
Je viens de la faire ^^
Alors je t'épargne tous les calculs (oui, je suis flemmarde, c'est long d'écrire toutes les formules) mais en gros j'ai fait l'équation Em(M) = Em(B) et je trouve que 1/2 = cos et donc j'ai trouvé que =arccoss(1/2)= 60° !
C'est tout bon ?
En tout cas, merci beaucoup, tu m'as aidée à comprendre 😁
Mdr t'en fait pas j'avais déjà fait les calculs donc^^
Oui oui c'est correct
Derien
Bonne continuation !
Bonjour 😊,
J'ai un DS sur les énergies mécaniques dans une semaine et j'aimerai savoir comment êtes vous parvenus à ces résultats?
Merci d'avance
Re bonjour
Je ne trouve pas Quels sont les calculs pour passer de Em(M)=Em(B)=Em(C) pour trouver la formule racine carré de g ect ...
Et ceux du Em(M)=Em(B)
Impossible d'y parvenir 😔
Ah d'accord je comprend mieux !^^
Tu veux que j'essaie de te mettre sur la voie, ou tu préfères que je te donne toutes les étapes directement ?
C'est toi qui voit
Les résultats, je pense que ça me permettrai de comprendre mes erreurs de calculs..
Merci beaucoup ! 😊
Okai^^
Alors tu sais que :
- Em(M) = Em(B) (c'est pas la peine de passer par le point C )
- Ec(B) = 0
- le pendule a une longueur l au niveau de M, et une longueur l/2 au niveau de B
Tu obtiens donc l'équation : mgl(1- cos)+ 1/2mvM² = mgl/2(1 - cos(90°))
mgl(1- cos)+ 1/2mvM² = mgl/2
2gl(1- cos)+ vM² = gl (on multiplie par 2 et on divise par m)
vM² = gl - 2gl(1- cos)
vM = (gl - 2gl(1- cos))
En remplaçant l par 1 et par 40, tu obtiens l'équation de Titouille
Tu peux même simplifier encore un peu et trouver :
Pour la deuxième question, au lieu de calculer vM à partir de , tu fais l'inverse^^
Donc tu pars de la même relation :
vM = (gl(2cos - 1)) = 0 (c'est mieux de remplacer vM par 0 dès le début^^)
gl(2cos - 1) = 0
2cos - 1 = 0
cos = 1/2
= cos-1 (1/2)
Voilà
Annuler
connectez vous