Inscription / Connexion Nouveau Sujet
exercice sur la largeur d'une fente
Je dois faire un devoir maison durant ces vacances; j'ai commencé mais la je bloque sur les question suivantes (à partir de d) pouvez-vous m'aider ?
voici l'énoncer complet :
On cherche à mesurer la largeur d'une fente utilisée dans un spetroscope et à vérifier le paralléllisme des bords. Pour cela, on commence par réaiser ds figures de diffraction avec des fils de différents diamètres et un laser. Le tableau suivant donne la largeur de la tache centrale de diffraction en fonction du diamètre du fil.
largeur L (mm) 64 26 16 11 8
diamètre d (mm) 0,02 0,05 0,08 0,12 0,16
1/d (mm⁻ 1) 50 20 12,5 ≈8,3 6,25
a) Recopier le tableau puis compléter la dernière ligne (fait : chiffres en gras)
b) Tracer le graphique donnant la largeur L de la fente en fonction de 1/d. On prendra 1cm pour 5mm-1 et 2cm pour 10 mm
(fait, j'ai mis le rapport 1/d en abscisse et L en ordonnée)
c) quelle est l'allure du graphique ? (c'est un droite passant par l'origine du repère)
d) montrer que L peut se mettre sous la forme L= k/d et calculer la valeur de d (là je sèche)
e) on envoie maintenant le faisceau laser au centre de la fente de largeur inconnu. La tache centrale de la figure de diffraction mesure 20mm.
Sachant que la figure de diffraction obtenue avec une fente de largeur d est la meme que celle d'un fil de meme diamètre, calculer la largeur de la fente. (là non plus je ne sais pas je pense qu'il faut avoir fait le d) pour répondre)
Comment procéder pour vérifier le parallélisme des bords ? (Je n'en ait aucune idée !)
Aider moi s'il vous plait !
Salut,
a. Ok
b. TB
c. TB !
d. Si la courbe L = f(1/d) est une droite passant par l'origine, L et 1/d sont proportionnels. Si on appelle k cette constante de proportionnalité, on a la relation : L = k.1/d = k/d.
Remarque : k est aussi le coefficient directeur de la droite.
=> à déterminer.
Regarde la fiche sur la diffraction (modèle ondulatoire de la lumière) dans la section terminale.
je ne comprend pas comment calculer k car si je me contente de faire k=L*d, je n'obtient pas les memes valeurs partout :
exemple L= 64 et d=0.02 k=64*0.02=1.28
mais lorsque L=26 et d=0.05 k=26*0.05=1.3
et 1.28
1.3
Que dois-je en déduire ?
mais ce n'est pas le calcule qui me pose problème, c'est le résultat : lorsque j'utilise des valeurs différentes, k n'est pas le meme alors qu'il est sensée etre pareil pour toutes les valeurs
d'après mes calcules la droite ne passerais pas par l'origine ( pourtant elle y passe sur mon graphique) puisque L et d ne sont pas proportionel
mon problème est que selon les valeurs du tableau que j'utilise pour calculer k je n'obtient pas les meme résultat
ex : avec L=64 et d=0.02 on a k=L*d=64*0.02=1.28
avec L=26 et d=0.05 on a k=L*d=26*0.05=1.3
avec L=11 et d=0.12 on a k=L*d=11*0.12=1.32
avec L=16 et d=0.08 on a k=L*d=16*0.08=1.28
avec L=8,0et d=0.16 on a k=L*d=8.0*0.16=1.28
quel valeur dois-je utiliser ?
C'est normal de ne pas obtenir une droite parfaite : ce sont des valeurs expérimentales. Il faut donc faire passer une droite par un maximum de point : c'est ce qu'on appelle faire une régression linéaire.
Tu peux faire par exemple la valeur moyenne des k trouvés.
Pour info sur la régression : je considère une expérience X (c'est un exemple qui n'a pas de rapport avec ton exo). On trace plusieurs points de mesures. On trace la droite qui passe par le plus de points :
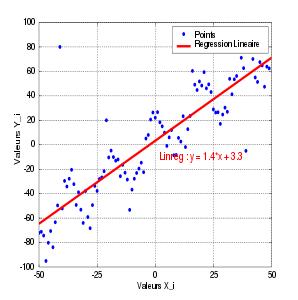
ça y est j'ai compris, merci beaucoup de ton aide ! pour la valeur de k j'ai obtenu environ 1.29
et pour le e) 1.29/20 
0.06mm
Par contre je ne comprend pas la question sur le parallélisme des bords.
peut-tu m'expliquer comment procéder pour vérifier le parallélisme des bords car je n'en ai aucune idée ?
Une solution éventuelle consisterait à vérifier si la tache de diffraction est bien symétrique...
Au passage, c'est toi qui a posté ceci ?
Oui, désolé mais vu que personne ne me répondait, j'ai voulu essayer sur un autre forum (j'était un peu désespérée de n'obtenir aucune réponse) mais en tout cas je te remecie énormément pour ton aide elle m'a été précieuse. et je ne ferait plus de multi-postes à l'avenir !
salut:
a) le tableau
largeur L (mm) 64 26 16 11 8
diamètre d (mm) 0,02 0,05 0,08 0,12 0,16
1/d (mm - 1) 50 20 12,5 8,3 6,25
b) le graphique donnant la largeur L de la fente en fonction de 1/d.
c) l'allure du graphique est une droite passant par l'origine du repère.donc son équation est de la forme :y=Kx c'est à dire:
k est le coefficient directeur.
d) donc L peut se mettre sous la forme L= k/d
calculons la valeur de k
donc : or
donc k=
e) L=20mm.
la fente de largeur d est la meme que celle d'un fil de meme diamètre,
c'est à dire
m
Salut 122155
c'est gentil d'avoir rédigé complètement cet exercice
Cela permet de vérifier nos résultats et heureusement on a trouvé les même à l'arrondi près.
salut gbm
je rappel cette belle expression postée par lafol (sur l'île des mathématiques) quand ceci se produit : "Avec deux lampes, il y a moins d'ombre".
et dans l'île de physique avec plusieurs lampes il n'y aura plus d'ombre.
bon après midi .
Merci beaucoup de votre aide 122155 et gbm grace à vous la physique ne me parait plus aussi obscure !
oui, on m'a parler de vérifier la symétrie de la tache mais je n'ai pas bien compris comment proceder
Sachant que la figure de diffraction obtenue avec une fente de largeur d est la meme que celle d'un fil de meme diamètre,on trouve la largeur de la fente.
et si les résultats sont les memes ,les bors de la fente sont bien parrallèles entre eux donc cette étude nous a permet de detrerminer la largeur de la fente et de vérifier le paralléllisme de ses bords.
Annuler
connectez vous