Inscription / Connexion Nouveau Sujet
exercice sur l'energie mécanique
Bonsoir!
J'aimerais que vous m'aidiez à traiter mon exercice de physique dont le contenu est le suivant:
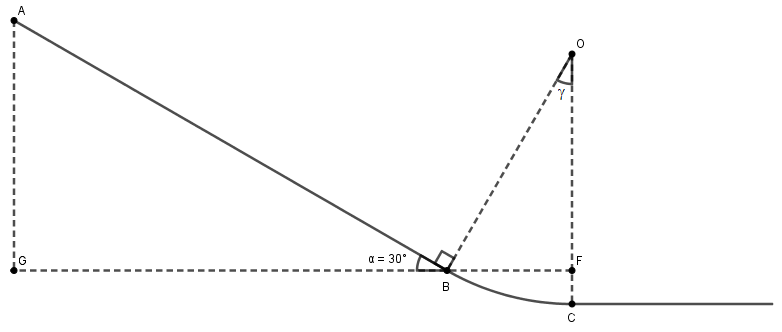
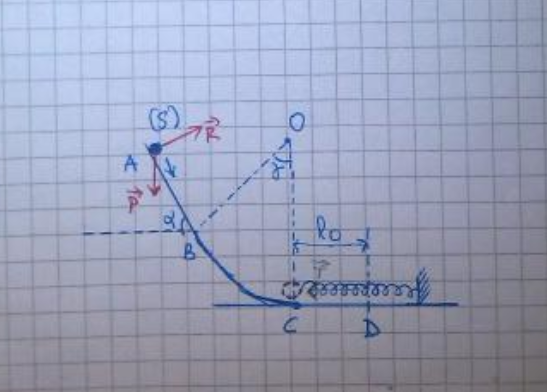
Un Solide S glisse d'une pente comme l'indique le schéma ci-dessous. Les frotements sont négligeables sur AB et BC. Mais ils sont assimilés à une force f constante sur le tronçon CD.
1) Enoncer le théorême de l'énergie cinétique.
2) Appliquer ce théorême , calculer la vitesse de la bille au point B et C.
3) En C, on place un ressort de raideur K=200N/m. La bille heurte le ressort à une vitesse Vc qu'elle comprime d'une longueur L0=25cm jusqu'au point D.
a) Enoncer clairement le principe de conservation de l'énergie mécanique.
b) ce principe est il verifié sur CD? Pourquoi?
Montrer que K*L0²+2L0*f+mVc²=0
c) déduire m.
4) Supposons maintenant que la bille n'est plus ponctuelle. Son rayon R=2cm.
Exprimer la nouvelle vitesse au point B en supposant que la masse n'a pas changé.
a(alpha)=30° , AB=L=2.5m ,r=OB=OC=1.25m , f=2N , K=200N/m L0=25m
Voici ce que j'ai debuté:
1) «la variation de l'énergie cinétique d'un solide dans un intervalle de temps donné est égale à la somme algébrique des travaux de toutes les forces extérieures appliquées à ce solide pendant cet intervalle de temps.»
2) soit Q cette variation .
Pour le système on a donc :
Q= P+R+T (avec vecteur sur les forces) = Ec(C)-Ec(A).
*Calcul de la vitesse au point B:
Ec(B)=½mV²(B)
==>V²(B)= 2*Ec(B)
Mais je ne sais pas comment avoir Ec en B pour avancer ...
Merci d'avance.

Question 2 :
Deux forces s'exercent sur S entre A et B :
Le poids de S et la réaction
de la pente.
Le théorème de l'énergie cinétique permet d'écrire que :
En supposant que S parte sans vitesse initiale ( l'énoncé ne dit rien à ce sujet ) cette relation permet d'obtenir la vitesse de S en B
Un calcul similaire permet d'obtenir la vitesse de S en C
Question 2 :
Deux forces s'exercent sur S entre A et B :
Le poids
Le théorème de l'énergie cinétique permet d'écrire que :
En supposant que S parte sans vitesse initiale ( l'énoncé ne dit rien à ce sujet ) cette relation permet d'obtenir la vitesse de S en B
Un calcul similaire permet d'obtenir la vitesse de S en C

Bonjour, s'il vous plaît pouvez vous essayer de montrer comment avoir la Vitesse en B à partir de cette expression?
On part de :
On fait l'hypothèse que VA=0 (départ arrêté) donc que EcA=0
On exprime EcB en fonction de m (masse de S) et de VB
On exprime le travail du poids de S en fonction de m, g, L et α
On démontre que le travail de la réaction de la pente est nul.
On en retire une équation dans laquelle la seule inconnue est VB
On exprime à partir de cette équation VB en fonction de g, L et α
V(B) = 5,0 m/s OK
Tu trouves une vitesse en C inférieure à celle obtenue en B
Curieux non ?
Et comme tu ne détailles pas ton calcul je ne peux pas t'en dire davantage.
Cependant c'est la question 3-b qui me dérange un peu que faut-il faire probablement...
Je sais que
?
V(B) = 5,0 m/s OK
Tu trouves une vitesse en C inférieure à celle obtenue en B
Curieux non ?
Et comme tu ne détailles pas ton calcul je ne peux pas t'en dire davantage.
ok... Je pense que la vitesse a un peu dimunié en C comme la pente à tendance à s'applatir ou bien?
Comment as tu trouvé que V(C) = 4,36m/s ?
Est ce une simple erreur de calcul ou autre chose ? Je ne sais pas.
C'est bien pour t'aider à situer ton erreur que je te demande depuis un bon moment de donner le détail du calcul qui t'a amené à 4,36m/s
On a : Ec(C)-Ec(B)=W(P) sur BC .. ==> Ec(C)=W(P) sur BC + Ec(B)
On sais que Ec(C)=1/2mV²C
Ec(C)=Ec(C) <==> 1/2mV²C =m*g*sin@*R*@+1/2mV²B
J'ai tiré Vc=√2*g*sin@*R*@+½V²(B) . le tout dans la racine
≈4,36m/s
Je n'arrive pas à démontrer Klo²+2lof+mV²C=0
J'essaye de remplacer chacun par sa valeur mais je n'ai m ...