Inscription / Connexion Nouveau Sujet
Exercice Physique : Travail et Puissance
Bonsoir,
Depuis deux jours, je suis bloqué sur un même exercice et j'aimerai avoir sa résolution complète SVP.
Voici l'énoncé :
1- Couché sur le sol horizontal, une colonne cylindrique en marbre, de longueur L = 3,00 m, de rayon
r = 0,30 m, de masse volumique 2200 kg.m-3 doit être dressée verticalement Calculer le travail W1 nécessaire pour effectuer cette manœuvre.
2- On dispose maintenant de n cylindres en marbre de rayon r chacun, constitué du même matériau que la colonne, posés tous sur le sol horizontal. Mis les uns les autres, ils forment une colonne de longueur L, semblable à celle de la question 1. Calculer le travail W2 nécessaire pour effectuer ce montage. AN : n =10
3-comparer W1 et W2. Commenter.
Bonjour,
Le règlement de ce forum interdit de faire à la place des élèves le travail qui leur est demandé.
En revanche on se propose de t'aider à partir de ton travail personnel.
Je suggère que tu publies ce que tu as obtenu au cours des deux jours de travail que tu as consacré à cet exercice.
Même faux, ce travail initial permettra de mieux comprendre la nature de tes difficultés.
Voici ce que j'ai pu faire...
1.) Calculons le travail nécessaire W1 pour effectuer cette manoeuvre.
W1= -mgh or m=
x V et V =
x r2 x L et h = (L/2 - r)
Donc W1= - x x r2x L x g x (L/2 - r)
Convertissons la masse volumique en Kg/L
= 2200Kg/m3 = 2,2Kg/L
A.N. : W1= -2,2 x x 0,32 x 3 x 10 x (3/2 - 0,3)
W1= -22,39J
Deux remarques concernant ce que tu as fait :
1) La question porte sur le travail à fournir pour soulever la colonne et non sur le travail du poids de cette colonne.
Il en résulte que ce travail est opposé à celui que tu as calculé.
W1 = mgh = * * r2 * L * g * (L/2 - r)
2) Application numérique : Pour obtenir le résultat en Joules, il faut conserver la masse volumique en kg/m³
Et puis quelques détails :
L'énoncé ne précise pas la valeur à utiliser pour "g"
Dans ce cas il vaut mieux prendre g = 9,8 N/kg
Le symbole de l'unité de masse n'est pas le Kg mais le kg
D'abord merci pour vos interventions et quelques remarques importantes.
Pour calculer la masse d'une colonne sachant qu'on a sa masse volumique et qu'on peut obtenir son volume , il faut utiliser la formule:
m= x V avec V= r2 x L
D'où m= x r2 x L.
Ensuite pour le travail W1 est-ce que je dois appliquer la formule W1= 
.AB(vecteur) ?
Tu as déjà trouvé (au signe près) l'expression de W1 :
W1 = mgh = * * r2 * L * g * (L/2 - r)
Il te reste seulement à revoir l'application numérique.
odbugt1 D'accord. Merci.
Maintenant concernant la question 2, je peux resoudre de la meme maniere que le 1) mais en changeant la hauteur et le signe (si nécessaire) pour chaque travail de la force pour un cylindre.
W2 =W1 +W2'+W3 ... +W10
W2=mg(h1 +h2 ...+h10)
Tout ceci étant un peu long et minutieux, est-ce qu'il n'y aurait pas une expression mathématique pouvant simplifier les calculs en écrivant le travail W2 en fonction de n ? SVP?
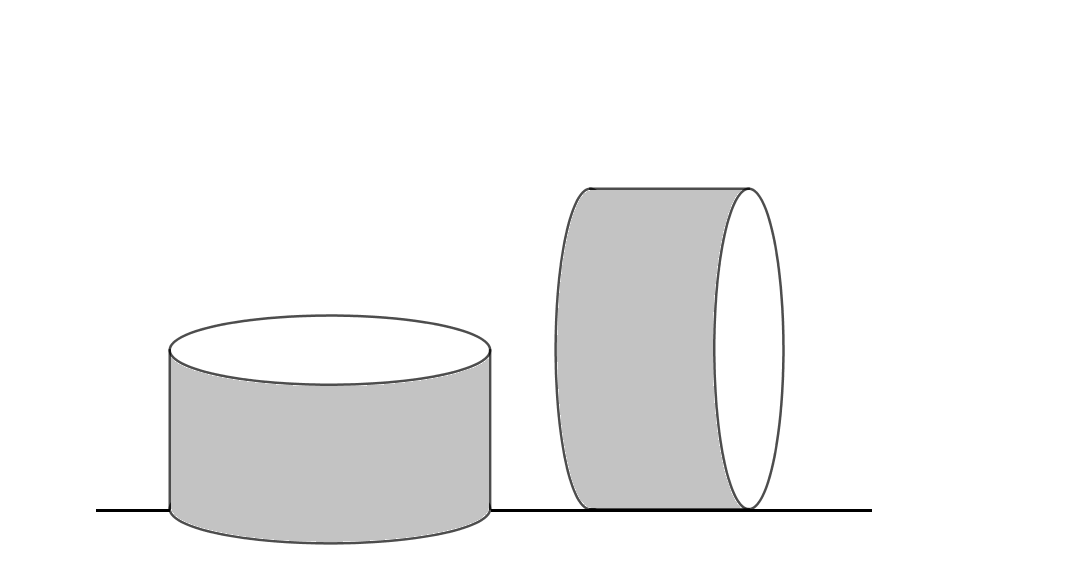
Le calcul dépend de la position initiale des cylindres de marbre.
Sont ils en contact avec le sol selon une face circulaire ou selon une face latérale ?
Ton énoncé n'en dit rien.
La figure ci dessous représente les deux cas et respecte l'échelle dans le cas ou n=10 pour lequel la hauteur de chaque cylindre (30cm) est égale à son rayon
Annuler
connectez vous