Niveau première

Exercice mécanique : j'ai pas compris

Posté par
AsPiraTeuRe 09-12-15 à 15:50

Bonjour,

J'ai un exercice que nous avons fait tous seul mais que notre prof ne nous à pas faire une correction en classe mais nous a donné une correction par internet. Malheureusement, elle ne détaille pas ses calcules. Pouvez-vous me les expliquer.

Voici l'énoncé :
A la piscine, Jonathan veut atteindre avec un ballon sa copine perchée sur un plongeoir à la hauteur h=3.00m au dessus du point de lancer O. Le ballon est lancé en O, avec une vitesse initial $\vet{Vo}=10 m.s^{-1}$ , dirigée vers sa copine avec un angle de tir = 30°
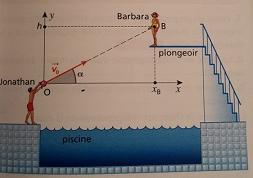
$Exercice mécanique : j\'ai pas compris$

A l'instant où le ballon part, la fille se laisse tomber dans la piscine.
Déterminer les équations horaires du mouvement du ballon, puis l'équation de sa trajectoire.

J'ai réussit à faire les équations horaires du mouvement du ballon.

$\vec{a(t)}\left\lbrace\begin{array}l Ax(t)=0 \\ Ay(t)=-g \end{array}$

$\vec{v(t)}\left\lbrace\begin{array}l Vx(t)=Vo* cos(\alpha) \\ Vy(t)=-g* t+Vo *sin(\alpha) \end{array}$

$\vec{Og(t)}\left\lbrace\begin{array}l x(t)=Vo*cos(\alpha)*t\\y(t)=\frac{-g*t²}{2}+Vo*sin(\alpha) \end{array}$

Puis après, nous avons, sans aucune explication, :

$Y(x)=\frac{-1}{2} \times \frac{g}{Vo² \times cos²(\alpha)} \times x² + tan(\alpha) \times xb$ .

Donc pouvez-vous m'expliquer comment on a se calcule ?

Je vous remercie d'avance.

***Edit gbm : image recadrée et niveau mis en accord avec ton profil***

Posté par re : Exercice mécanique : j'ai pas compris 09-12-15 à 16:59

Bonjour.

De l'expression     $x = V_0  t  cos  \alpha$      on tire :     $t  =  \dfrac{x}{V_0  cos  \alpha}$

En remplaçant $t$ par la valeur précédente dans l'expression :     $y = - \dfrac{g}{2}  t^2  +  V_0  t  sin  \alpha$      on obtient :

$y = - \dfrac{g}{2} ( \dfrac{x}{V_0  cos  \alpha})^2  +  V_0 ( \dfrac{x}{V_0  cos  \alpha})  sin  \alpha$

Après simplification par $V_0$ dans le second terme, on obtient :

$y = - \dfrac{g}{2  {V_0}^2  cos^2 \alpha}  x^2  +   x   \dfrac{sin  \alpha}{ cos  \alpha}$

Comme : $\dfrac{sin  \alpha}{ cos  \alpha} = tan  \alpha$

on peut écrire, finalement :

$y = - \dfrac{g}{2  {V_0}^2  cos^2 \alpha}  x^2  +   x   tan  \alpha$

OK ?

Posté par re : Exercice mécanique : j'ai pas compris 09-12-15 à 18:13

D'accord. Je vous remercie

Posté par re : Exercice mécanique : j'ai pas compris 09-12-15 à 18:28

Je vous en prie.
Au revoir.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau première
46 fiches de physique - chimie en première disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Exercice mécanique : j'ai pas compris

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique