Inscription / Connexion Nouveau Sujet
exercice lois de réfraction
Bonsoir, pourriez vous m'aider pour cette exercice ? merci d'avance
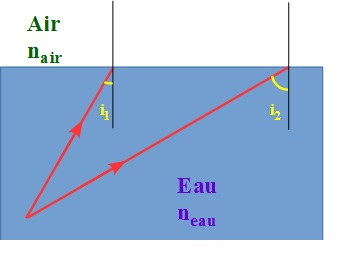
Un homme grenouille dirige la lumière de sa torche vers la surface de l'eau. On s'intéresse à la marche des deux rayons de lumières extrêmes émis par la lampe torche. L'un des rayons arrive avec un angle i1=30° sur l'interface eau/air, l'autre arrive avec un rayon i2= 60°.
1)Quel est l'angle de réfraction r max possible ? Quel angle d'incidence limite correspond a cette angle de refraction.
2)Qu'arrive-t-il au rayon 1 et 2 (pas de calculs supplémentaire)
Les valeurs des indices de réfraction de l'eau et de l'air doivent sans doute être indiquées dans l'énoncé.
En ce qui concerne la façon d'utiliser la loi de S-D, je vous renvoie à l'autre topic que vous avez posté.
Ces deux angles sont mesurés dans l'eau.
Sous quel angle chacun de ces rayons émerge-t-il (s'il émerge !) dans l'air ?
Est ce qu je dois faire comme ceci
n1*sin(ai)=n2*sin(ar)
Ou n1*sin(ar)=n2*sin(ai)
Puisqu'il s'agit d'une interface ou n1=eau et n2l'air
Il faut faire un schéma et adapter vos notations à la situation de l'exercice.
Ici les deux milieux transparents sont : l'eau, d'indice neau 
1.33 (vérifiez quand même cette valeur dans l'énoncé) et l'air, d'indice nair 1.
Vous aurez à écrire deux fois la loi de Snell-Descartes, une fois pour le rayon 1, qui tombe sur le dioptre sous une incidence i1 = 30°, puis, une seconde fois pour le rayon 2, qui tombe sur le dioptre sous une incidence i2 = 60°.
Vous déterminerez ainsi les éventuels angles de réfraction : r1, pour le rayon 1, puis r2, pour le rayon 2.
Au boulot !
R1
C'est :
1*sin(30°)=1,33*sin(ar)
0,5=1,33*sin(ar)
Sin(ar)=0,5/1,33=0,37
Arcsin(0,37)=21,7°->22°
Ou
1,33*sin(30°)=1*sin(ar)
1,33*0,5=sin(ar)
Sin(ar)=0,6
Arcsin(0,6)=36,8°->37°
C'est :
1*sin(30°)=1,33*sin(ar)
Mais non ! Un peu de logique enfin !
Dans quel milieu l'angle de 30° est-il mesuré, l'air ou l'eau ?
Quel est l'indice de réfraction du milieu dans lequel on mesure les 30° ?
1,33*sin(ai)=1*sin(ar)
donc r1=37°
sin r1 = 1.33 sin i1
sin r1 = 1.33 sin 30° sin r1 = 0.655
Soit : r1 = arcsin (0.665) = 41.7°
42°
Ah oui donc r2=90°
sin r2 = 1.33 sin i2
sin r2 = 1.33 sin 60° sin r2 1.152
Réfléchissez à ce résultat et concluez.
Merci j'ai rectifié ceci j'ai refais le calcul en tant precis je trouve bien ves 2 résultats
Pour r2 le rayon n'est plus refracté mais reflechi car ar>90° alors que pour qu'il y est le phenomene de réfraction il faut que i>r
Pour r2 le rayon n'est plus réfracté mais réfléchi
car ar>90° alors que pour qu'il y est ait le phénomène de réfraction il faut que i>r
C'est faux bien évidemment.
L'application de la loi de S-D au rayon 2, pour la réfraction, conduit à : sin r2 = 1.152 ce qui, mathématiquement, est impossible.
Le rayon 2 ne passe donc pas de l'eau dans l'air, il est totalement réfléchi par le dioptre eau/air qui se comporte comme un miroir et le renvoie dans l'eau.
Pour l'angle limite, regardez le schéma ci-dessous.
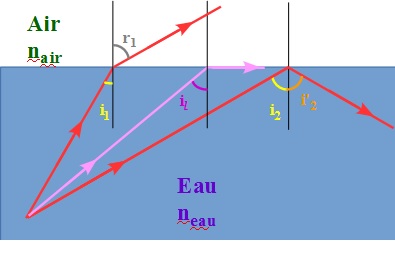
Le rayon correspondant à l'angle limite il est représenté en rose, sous quel angle émerge-t-il dans l'air ?
Que donne alors la loi de S-D ?
Avant de trouver il, il faut donner la valeur de l'angle de réfraction maximale rmax ; une simple lecture sur le schéma suffit, aucun calcul n'est nécessaire pour rmax.
1,33*sin(ai)=1*sin(ar)
1,33*sin(ai)=1
Sin(ai)=1/1,33=0,7518
Arcsin(0,7518)=49°
J'ai arrondi le résultat
C'est bon, vous y êtes arrivé !
Avez vous compris le phénomène de réflexion totale et la signification de l'angle d'incidence limite ?
Annuler
connectez vous