Inscription / Connexion Nouveau Sujet
Exercice énergie cinétique et travail des forces
Salut à tous,
Je n'arrive pas à résoudre cet exercice :s
Enoncé :
Manon circule en rollers et aborde le bas d'une pente inclinée d'un angle 
=5° par rapport à l'horizontale avec une vitesse initiale V0=12km/h en suivant la ligne de plus grande pente.
Manon se laisse glisser sans manoeuvrer. On peut alors la modéliser par un solide en mouvement de translation.
Données :
Masse de manon = 45kg et on prends g=10N/kg
a. On néglige les frottements. Calculer la distance maximale que Manon peut parcourir avant de redescendre.
b. La distance effectivement parcourue avant l'arrêt est d=4,5m. On modélise les frottements par une force unique opposée au déplacement. Calculer f
________________________________________________________________________________________________________
J'ai essayé de procèder comme ceci :
a. Le solide n'est soumis qu'à une seule force : le poids .
WAB() = m * g * (ZB-ZA)
Mais je ne sait plus trop quoi faire :s
a)
Soit d la distance que parcourt Manon dans la montée:
Travail du poids de Manon sur la montée: WP = -mgd.sin(alpha) = - 45 * 10 * d * sin(5°) = -39,22 d
Energie cinétique de Manon en bas de la côte: Ec1 = (1/2)m.V1² = (1/2)*45*(12/3,6)² = 250 J
Energie cinétique de Manon au point le plus haut atteint: Ec2 = 0 (puisqu'en cet endroit la vitesse de Manon = 0)
On a Ec1 - Ec2 + WP = 0
250 - 0 - 39,22 d = 0
d = 250/39,22 = 6,4 m
La distance maximale que Manon peut parcourir avant de redescendre est de 6,4 m
-----
b)
Travail du poids de Manon sur la montée: WP = -mgd.sin(alpha) = - 45 * 10 * 4,5 * sin(5°) = -176,5 J
Energie cinétique de Manon en bas de la côte: Ec1 = (1/2)m.V1² = (1/2)*45*(12/3,6)² = 250 J
Energie cinétique de Manon au point le plus haut atteint: Ec2 = 0 (puisqu'en cet endroit la vitesse de Manon = 0)
Travail des forces de frottement sur la montée: Wf = f*d = f * 4,5 = 4,5 f
On a : Ec1 - Ec2 + WP + Wf= 0
250 - 0 - 176,5 + 4,5f = 0
f = -16,3 N
-----
Sauf distraction. Vérifie les calculs et essaie de comprendre 
Salut,
Merci de votre réponse,
Je ne comprends pas une chose (formule qui n'est pas dans mon cours):
WP = -mgd.sin(alpha)
Comment est-ce qu'on la démontre ? Je supose que 'd' est la longueur
Le travail du poids de Manon est WP = m * g * (ZB-ZA)
(ZB-ZA) est la différence d'altitude entre les points d'arrivée (en haut) et de départ.
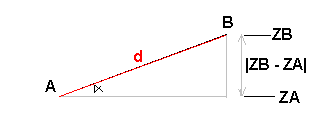
Dans le triangle, on a:
|ZB - ZA| = d.sin(alpha)
et en tenant compte que Zb - ZA < 0 (puisque ZB > ZA), on a :
(ZB - ZA) = - d.sin(alpha)
WP = m * g * (ZB-ZA)
WP = - m * g * d.sin(alpha)
-----
OK ?
C'est dans la partie a, sans frottement, qu'on trouve d = 6,4 m
Mais dans la partie b, avec les frottements, la distance parcourue en montée est 4,5 m (précisé par l'énoncé).
Bonjour, j'ai compris votre démarche et vos explications qui sont trés bien !
Mais il y a une chose que je ne pige pas !
b)
Travail du poids de Manon sur la montée: WP = -mgd.sin(alpha) = - 45 * 10 * 4,5 * sin(5°) = -176,5 J
Energie cinétique de Manon en bas de la côte: Ec1 = (1/2)m.V1² = (1/2)*45*(12/3,6)² = 250 J
Je ne comprend d'ou vien le 3.6 ??
Pourrait-on m'expliquer svp
Merci d'avance !
Les calculs sont faits en unités SI et l'unité SI pour une vitesse est le m/s et pas le km/h
v = 12 km/h ---> v = (12/3,6) m/s
Sauf distraction.
Annuler
connectez vous