Inscription / Connexion Nouveau Sujet
exercice d'optique : la méthode de Bessel
Bonjour,
mon professeur de physique nous a donné cet exercice a résoudre et ... bien que je potasse dessus depuis des lustres je n'arrive pas a le resoudre : pourriez vous m'aider, me donner des pistes ...
merci d'avance
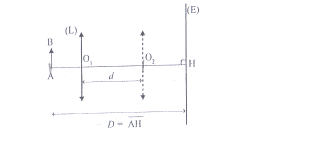
La méthode de Bessel est une méthode expérimentale de détermination de la distance focale f' d'une lentille convergeante L de centre optique O. Pour mettre en oeuvre cette méthode, on dispose d'une banc optique sur lequel un objet plan AB et un ecran E parallèle à AB sont séparés par une distance fixe D. On déplace la lentille L, de distance focale inconnue, de telle manière que son axe optique soit confondu avec la normale (AH) à l'écran passant par le point objet A. On remarque qu'il existe deux positions de O, notées O1 et O2 qui donnent une image nette A'B' sur l'écran.
1- montrer que OA obeit a l'équation du 2 degre suivante :
OA²+D.OA+f'.D=0
2-a quelle condition l'équation précédente ademt elle deux solutions distinctes ? on notera 
le discrimant de l'équation
3 etablir en fonction de D et de l'expression de ces 2 solutions notées O1A et O2A et telles que O1O2 = d 
0
4 en deduire l'expression f' en fonction de D et d
en deduire l'xpression de O1A et O2A en fonction de D et d
5 etablir en fonction de D et d, l'expression de grandissemnt 
1 et 2 correspondant respectivement au position O1 et O2 du centre optique de la lentille Quelle est la relation entre ces 2 grandissement ?
6 determiner la valeur de f', 1 et 2 sachent que d=11.2cm lorsque D=25.0 cm
...merci de votre aide
Bonjour,
Avec des énoncés légèrement différents ce problème est posté une dizaine de fois chaque année.
Utilise la fonction "Recherche" et tu trouveras de nombreux problèmes identiques et corrigés.
Pour apprendre à te servir du moteur de recherche : 
Pour faire ta recherche :
Clique sur les maisons, ce sont des liens !
merci je suis débutante je connais pas encore tres bien le site
je vais aller faire un tour sur tes liens ..
En voilà un : spé physique : focométrie des lentilles minces convergentes...
Mais en t'attendant, j'ai entièrement fait le tien... donc, si tu as des questions de compréhension !
Coll merci
mais je n'arrive pas a trouver des réponses satisfesant : les autres énoncés ne traitent pas vraiment la meme chose ...
L'objet et l'écran doivent être à une distance invariable D =AH
La relation de conjugaison donne 1 / O A' - 1 / OA = 1 / f '
Donc 1 / AH - 1 / OA = 1 / f '
soit ...
Il n'est pas sûr que je puisse t'aider cet après-midi.
Fais très attention aux signes !
Pour la question 1 :
et donc
2) = D2 - 4f '
et donc
D > 4f ' pour avoir deux positions distinctes
3) d = 
4) f ' = (D2 - d2)/(4D)
et
5) 1 = (D + d)/(d - D)
2 = (D - d)/(-D - d)
1 
2 = 1
pas grave
je vais étudier tt çà de + près
merci
c'est impressionnant le nombre de fois que tu as fait se sujet ...
Pour information :
quand = 4f ' cette méthode se nomme alors la méthode de Silbermann ; les deux positions de la lentille sont confondues en une seule et l'image (inversée) est de même taille que l'objet ; c'est une autre méthode de focométrie, mais alors la distance D n'est plus invariable ; la méthode de Bessel est plus facile à mettre en œuvre sur un banc d'optique. De plus en variant la distance D on peut la recommencer et ainsi améliorer la connaissance de f '
Je dois me déconnecter. Bon travail. Je te lirai éventuellement en fin d'après-midi.
Il faut maintenant résoudre l'équation du second degré.
En portant toujours une grande attention aux signes !
Puisque
et que
alors
en fait je ne voit pas la relation entre cette réponse au 3) et celle donné a 15h15 pour la meme question ...
Ce que j'ai écrit à 17h58 le 9 permet de ne pas se tromper dans les calculs de et de
et ensuite d'en déduire la valeur de d puisque
peut etre ai je trouvé :
O1A = - D +( D 2 - 4 D . f' ) / 2 et O2A = - D - ( D 2 - 4 D . f' ) / 2
soit d =
pourtant je crois qu'il manque qq chose mais je ne voit pas ou ...
pour le 4)
soit d = ( D 2 - 4 D . f' )
et en élevant au carré d2= D2 - 4 D . f'
Soit f = ( D2 - d2 ) / 4.D
apres pour O1A et O2A c'est encore un mystère
pour le 5)j'ai des problèmes dans mes étapes : ils m'en manquent ...
6) ...
Message de 20 h 02 : ce serait mieux avec les racines carrées !
Message de 20 h 34 : il manque encore une racine carrée et le mystère disparaîtra...
Question 5
A calculer deux fois ; une fois en remplaçant O par O1 et une deuxième fois en remplaçant O par O2
Question 6
Simples applications numériques !
effectivement : merci pour les racine carrés je savais bien que j'avais oublié qq chose !!!
d'accord je vais essyer de terminer ...
donc en effet, grace a ton aide j'ai pu résoudre la question 4 mais je peine a suivre tout ton résonnement sur la 5 ...
quoique je sais qu'il faut calculer :
avec la formule de 07h48 auj
se quie en fait doit donner :
1 = (D + d)/(d - D)
2 = (D - d)/(-D - d)
qd ceci est fait je doit trouver la relation 1 2 = 1
mais je ne sais comment l'obtenir ...
Comment l'obtenir ?
Tout simplement en faisant le produit 1 2 !
Les valeurs que tu as trouvées sont correctes. Tu as su faire attention aux signes.
OK merci 
c'était tout simple dsl je ne l'avait pas vu ...
je me lance donc dans le 6
et la je suis en train de recopier au propre le debut j'en suis au 4 et je suis en train de me poser la question : il est demande : "en deduire l'expression de O1A et O2A en fonction de D et d"
seulement moi j'arrive a deux expressionS pas a 1 expression 
d'accord merci
là je suis en train de recalculer le 5)
dois je mettre des intermediaire ou est ce que passe directement du calcul de sa :
a sa :
1 = (D + d)/(d - D)
2 = (D - d)/(-D - d)
Il ne faut jamais oublier d'intermédiaires. On doit pouvoir suivre ton calcul sans se poser de questions sur la manière dont tu as calculé.
d'accord je comprend
cependant c'est un peu problématique je n'ai pas noté mes calculs intermédiaire pourle 5)
je galère un peu
je le fais pour un pour l'instant :
1= OA'/OA = O1H/O1A = ?/((-D-d)/2)
je ne me souviens plus comment trouver O1H pourrai tu seulement me donner une piste j'aime comprendre et trouver par moi meme
1 = oh/oa = O1H/O1A = (o1o2 + o2h) / ((-D-d)/2) = (d+(AH - AO2))/ ((-D-d)/2) = d+(D-d) / ((-D-d)/2) = ?
je crois qu'il y a bcp de fautes ...
Ne sachant pas ce qu'est le point H je ne peux pas suivre ces calculs.
Je ne connais que O1, O2, A et A'
Merci d'en faire autant la prochaine fois ! H n'a aucun intérêt sur le plan de l'optique.
Puisque l'on déplace la lentille de façon à ce que sur l'écran apparaisse une image nette de l'objet AB, alors en H on a l'image de A qui se nomme A'
___________
J'écris et je répète depuis le début que tu n'as aucune chance de t'en sortir en optique géométrique si tu n'utilises pas les mesures algébriques ! !
et
Or tu as calculé
donc, c'est facile...
OK
je retiens pour les mesures algébriques, merci
pour la suite d'accord je n'avais pas vu ca sous cet angle ...
et donc 2 = o2a' / o2a
o2a' = o2a + aa'
o2a = (-D+d) / 2
C'est faux...
Le 9/10 à 15:15 je t'ai donné les réponses
Le 11/10 à 20:46 tu m'as dit avoir su faire la question 4
Comment veux-tu que je m'y retrouve ?
L'énoncé exige que O1O2 = d 0
Prends tes valeurs :
tu trouves O1O2 = -d
Tu n'as pas fait attention aux signes !
excuse moi je mis perd moi aussi ...
bon alors je reprend :
oui j'ai su faire la quest 4 )
j'ai trouvé les resultats précdent mais en fait je crois que j'ai inversé o1a et o2a
si je remet tt ds l'ordre cela donne :
o1a : (-D+D) /2 et pour o2a : (-D-d)/2
et la je rejoint tes resultats a toi et donc :
o2a = (-D-d)/2
je suis encore une fois dsl
Annuler
connectez vous