Inscription / Connexion Nouveau Sujet
Exercice coordonnés par latitude et longitude
Bonjour, j'ai besoin de votre aide pour l'exercice suivant :
On a 2 points A et B situés à la surface de la Terre et de coordonnées géographiques respectives : « 100° Ouest et 40° Nord » et « 42° Est et de 40° Nord ».
Questions :
1) Justifier que A et B sont sur le même parallèle ?
2) Tenter de montrer que la longueur du parallèle sur lequel sont situés A et B est de 30642 km (environ)
3) On a C le centre du parallèle où sont situés A et B, que vaut l'angle ACB ?
4) Calculer la longueur de l'arc de parallèle qui relie A et B?
Mes réponses :
1) Car ils ont la même latitude (40°Nord)
2) Seul question où je bloque vraiment.... Faut-il montrer par un calcul (si oui avec quel formule ?) où par des argumentations (Si oui de quoi faut-il parler ^^...)
3) ACB= 100°+42°= 142° ?
4) Je connais la relation suivante : L/ACB = Lc/360°
donc ici L = (142°*30.642)/360
donc L = 12086,5667?
Merci beaucoup si vous m'aidez ! 
Bonjour,
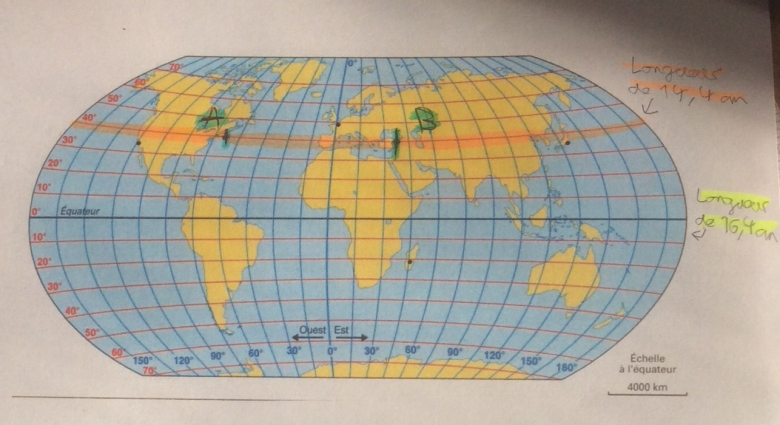
Pour la 2, faire un dessin en coupe de la Terre dans un plan contenant l'axe des pôles et le point A. A partir de ce dessin, déterminer le rayon du parallèle.
Pour la 4, OK, aux "détails" près de l'unité et du nombre de chiffre significatifs, votre distance est donnée à 10 cm près, avec des angles donnés au degré près !
Bonsoir merci pour votre réponse .
2) Est-ce que le placement de A et B sur un planisphère marqué par la longitude et la latitude marche également en mesurant le parallèle ? Je trouve que 1,8cm= 4000km et que le parallèle concerné mesure 14,4 cm. Donc 14,4 *4000: 1,8 = 32000 km...
Merci si vous répondez une nouvelle fois
Bonjour merci d'avoir fait ce graphique, mais j'avoue ne pas vraiment savoir quel type de calcul utilisé en ne connaissant que l'angle de 40° même si je suppose qu'il faut utiliser les formules trigonométriques....
Cependant en prenant le rayon de l'equateur et ces propriétés trigonométriques j'arrive à trouver une valeur approché de 30642 km dont voici le calcul :
Rayon de l'équateur / sin (40) = 31172,81618 km
Est-ce du pur hasard ?
Merci
C'est du pur hasard !
1- Vous partez d'un rayon pour arriver à une circonférence.
2- Vous divisez par un sinus inférieur à 1, donc la longueur du parallèle serait plus grande que la circonférence à l'équateur.
Ma figure me semblait parlante, donc détaillons : CA est le rayon de la terre, en appelant D l'intersection de l'axe des pôles et le segment horizontal qui est la trace du parallèle, DA est le rayon du parallèle. Donc rayon(parallèle)= ? et donc longueur(parallèle)= ?
Bonjour je n'arrive toujours pas ....
J'ai fait sin(50°)*6371 = 4880,469147 km....
Où 4880,4... km *2 = 9760,938294 km....
PS: 50° car 90°-40° ...
Merci si vous m'aidez à nouveau
4880 km est le rayon, donc la circonférence est ?
Remarque répétée : vous donnez une longueur au mm près avec des angles au degré près.
On rappelle qu'un mille nautique qui vaut 1852 m correspond à une minute d'un méridien.
Donc même si vous aviez des angles à la minute près, vous ne pouvez avoir mieux que le kilomètre.