Inscription / Connexion Nouveau Sujet
étude mécanique
Bonjour je bloque un peu sur cet exo (de DM)
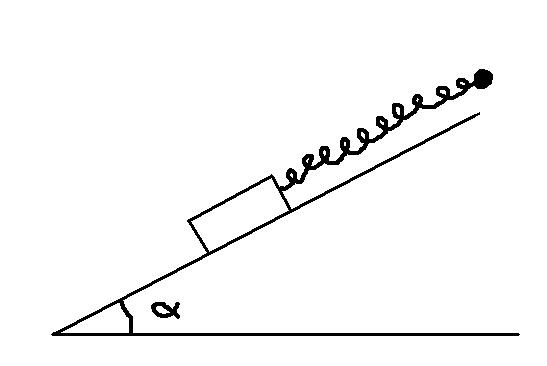
Guy s'interesse à un objet de masse m, glissant sans frottements sur un plan incliné d'un angle 
par rapport à l'horizontale. L'objet est accroché à un ressort de raiduer k et de longueur à vide l0, lui-même parallèle à la pente et accroché en haut de la pente à un point fixe.
A l'aide d'une étude mécanique de l'objet à l'équilibre, exprimer la longueur l du ressort en fonction de et des autres paramètres.
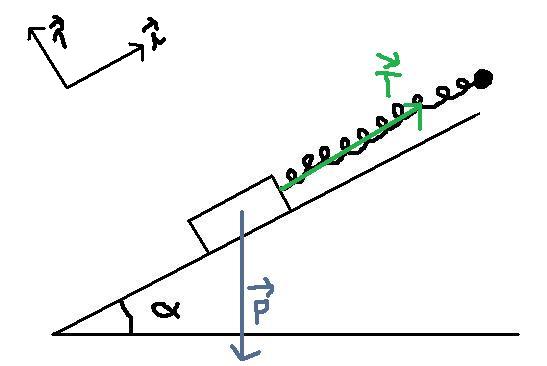
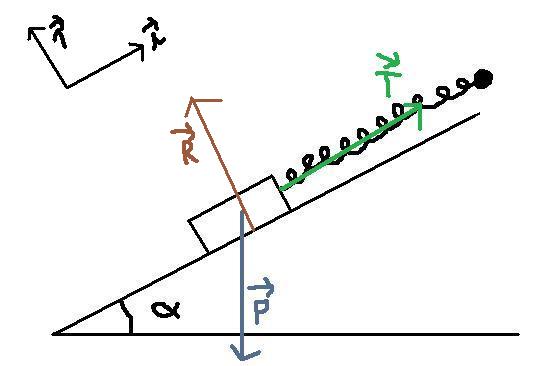
On étudie l'objet de masse m dans le réferentiel galiléen supposé terrestre ramené à son centre d'inertie. On munit le référentiel d'un repère orthonormé(0;
;
)où est parallèle au plan incliné et dirigé vers la droite et perpendiculaire au plan incliné et dirigé vers le haut.
Sur lui s'exercent :
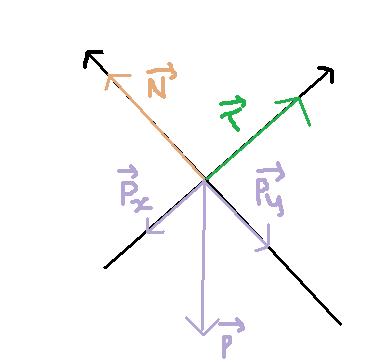
-son poids vectP = mvectg vertical vers le bas
-la tension du ressort vectT= k (|l-l0|)
Guy ! C'est bien d'essayer de renommer les personnages fétiches de ton professeur mais ça me fait rire... 
Tu as oublié une force dans ton bilan ! (sans cette dernière, l'objet passerait à travers le support...)
Et tu n'as pas besoin de valeur absolue pour la force exercée par le ressort : on peut la voir comme une grandeur algébrique. Si l'allongement est positif, alors l'objet est ramené vers le ressort et si l'allongement est négatif, l'objet est repoussé.
je trouve tout simplement le prénom Guy pitoyable 
(toutes mes excuses aux Guy!)
-vectT=k(l-l0) parallèle au ressort et au plan appliquée au point d'attache entre l'objet et le ressort et vers la droite
-la réaction du support vectR ?
sauf que vectR je peux pas le décomposer puisque l'objet glisse sans frottements, je le représente comment?
La réaction du support est perpendiculaire au support ici puisqu'il n'y a pas de frottement. Dans le cas général, elle se décompose selon une composante normale et une composante tangentielle. La composante tangentielle traduit les frottements ; elle est donc nulle ici.
-son poids vectP = m.vectg vertical vers le bas
-vectT=k(l-l0) parallèle au ressort et au plan appliquée au point d'attache entre l'objet et le ressort et vers la droite
-la réaction du support vectR ? de norme R
all right? avant de passer à la suite
All right
Je précise juste que tu aurais très bien pu représenter la force exercée par le ressort dans l'autre sens puisque son sens dépend du signe de l'allongement. Voir mon message de 16h26.
ensuite je cherche les coordonnées des vecteurs
vectT(k(l-l0);0)
vectR(0;R)
vectP hum c'est en fonction de mais je ne sais pas comment le retrouver ailleurs.. oui il faut faire de la trigo
Bon, on ne peut pas parler de produit scalaire donc on va faire autrement !
Au fait si tu regardes la suite de l'exercice, tu verras que la réaction normale du support est notée donc autant l'appeler tout de suite comme ça !
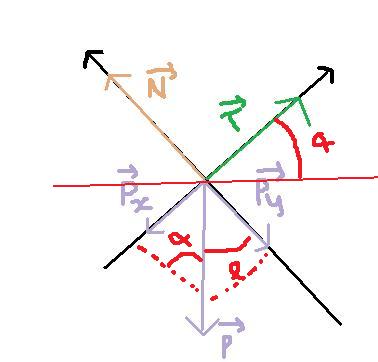
Pour la projection du poids, voir le schéma joint ! Le poids se décompose selon une composante parallèle au support (Px) et une composante perpendiculaire au support (Py). En faisant un peu de géométrie, tu peux montrer qu'on retrouve l'angle alpha là où je l'ai placé sur le schéma.
Écris ce que valent le cosinus et le sinus de alpha et tu pourras ainsi en déduiras les projections du poids.
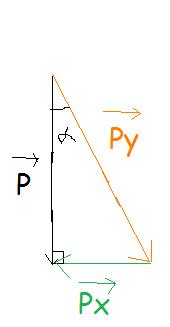
Regarde ton premier schéma, l'angle alpha est l'angle que fait le support avec l'horizontale.
Et on retrouve cette angle entre le poids et sa composante perpendiculaire au support (Py).
Maintenant, regarde MON schéma, et écris les expressions de cos(alpha) et sin(alpha) : ce qui est facile puisqu'on a un triangle rectangle.
cos(alpha) = ?
sin(alpha) = ?
(en fonction de P, la norme du poids, Px et Px les normes respectives des composantes tangentielle et normale du poids)
je suis habituée à faire ceci :
vectT(k(l-l0);0)
vectN(0;N)
vectP(-mgcos;-mgsin)
rectifie moi si besoin mais je pense pas
Oui c'est ça ! Tu as compris comment les retrouver ? Si tu as besoin des composantes du poids dans un autre exercice tu t'en sortiras ?
Voir ce schéma pour prouver qu'on retrouve bien l'angle alpha là où je te l'ai indiqué : 
.
Ah non c'est pas ça... C'est l'inverse...
Écris cos(alpha)=... et sin(alpha)=... en fonctino de Px, Py et P s'il te plaît.
Oui j'ai compris
merci beaucoup pour le schéma, tu es un dieu
L'objet est immobile donc on peut appliquer la première loi de Newton:
vectT+vectN+vectP= vecteur nul
sur (O;) cette égalité vectorielle donne:
k(l-l0)-mgcos=0
k(l-l0)=mgcos
kl -kl0 = mgcos
et ensuite il faut en extraire l c'est ça?
à partir de k(l-l0)=mgsin je vois pas comment simplifier
kl -kl0=mgsin
kl=mgsin+kl0
suis je sur le bonne voie?
l=(mgsin+kl0)/k
j'y pensais mais me retrouver avec une expression assez longue me paraissait bizarre
au fait penses tu que ton raisonnement à côté de ton schéma soit indispensable? Est ce bon si je fais mon schéma de 17:37 seulement?
Tu peux directement mettre qu'on retrouve alpha à cet endroit, pas besoin de justifier ça. Mon schéma c'était pour le justifier mathématiquement.
Oui, mais moi j'écrirais plutôt : .
énoncé du 2)
Dans la plupart des cas les frottements ne peuvent pas être négligés. Ainsi, dans la situation précédente, lorsqu'il y a des frottements non négligeables, il y a plusieurs valeurs de la longueur l du ressort pour lesquelles l'objet est au repos. Si on étire le ressort, il y a néanmoins une position lmax au-delà de laquelle on ne pourra plus avoir l'équilibre( et alors le ressort aura tendance à se contracter). Si on raccourcit le ressort, il y a une position lmin en-delà de laquelle l'équilibre n'est pas possible (et alors le ressort aura tendance à s'allonger).
Guy connait par ailleurs les lois de Coulomb du frottement. L'une d'entre elle dit que lorsqu'un objet est à la limite de glisser sur un support, la norme F de la force de frottements est proportionnelle à la norme N de la réaction normale : on écrit F=
N, où est le coefficient de frottement entre le support et l'objet.
A l'aide de deux études mécaniques séparées des deux situations limites (pour lmax et lmin) où cette relation est vérifiée et l'objet au repos, donner l'expression de lmax, puis lmin. En déduire l'expression de lmax-lmin, en fonction de m, g, k, et.
________
première étude mécanique pour lmax
On étudie l'objet de masse m dans le réferentiel galiléen supposé terrestre ramené à son centre d'inertie. On munit le référentiel d'un repère orthonormé(0;;)où est parallèle au plan incliné et dirigé vers la droite et perpendiculaire au plan incliné et dirigé vers le haut.Sur lui s'exercent :
-son poids vectP=m.vectg
-la force vectF de norme F=N force de frottements perpendiculaire au plan incliné et dirigée vers la droite
-la réaction normale vectN perpendiculaire au support de norme N=F/
jusque là ça va? je continue si c'est bon
Et le ressort dans tout ça ?
La force de frottement s'oppose au déplacement de l'objet donc revois le signe de cette force.
Je veux un schéma
En Sup, mon prof de maths disait : pas de dessin, pas de point ! Ça marche aussi pour la physique... surtout pour la physique !
"La force de frottement s'oppose au déplacement de l'objet donc revois le signe de cette force."
-la force ce frottements vectF de norme F=-N? pourtant sur le schéma vectF va dans le même sens que ...
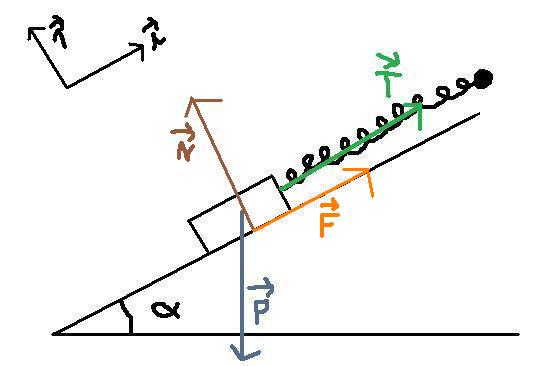
Attends, tu viens d'écrire une norme négative. Je ne t'ai pas dit de revoir la norme de la force de frottement mais son SIGNE.
La force de frottement s'oppose au déplacement. Or dans ce cas de figure, on étire le ressort : la force que le ressort exerce va donc tendre à ramener l'objet vers lui. L'objet monte donc la force de frottement, s'opposant à ce déplacement (la montée de l'objet), est suivant .
-la force vectF=N- de norme F=N force de frottements perpendiculaire au plan incliné et dirigée vers la droite
donc mon schéma est faux?
Non, ça ne va pas. Pourquoi perpendiculaire au support ? Tu l'as représentée colinéaire en plus : tu te contredis !
La force de frottement est colinéaire au support et opposée au déplacement du système.
Le ressort est étiré, la force exercée par le ressort va donc le ramener vers lui. Le système va donc "monter". On a dit que la force de frottement s'oppose au déplacement. Elle est donc colinéaire au support et vers la gauche (puisque le système va aller vers la droite !).
Tu comprends ou il faut que j'explique ça différemment ?
je comprends je confondais juste ^^
-la force vectF=N- de norme F=N
c'est juste au niveau des signes et des notations?
sur (O;)
le système est au repos donc la 1ère loi de Newton donne la relation :
vectT+vectF+vectN+vectP=vecteur nul
sur (0;) on obtient:
klmax=mgsin+N+kl0
lmax=(mgsin+N)/(k) + l0
Oui c'est juste mais si tu projettes aussi sur (O,) tu vas pouvoir trouver une relation entre N, m, g et alpha et ainsi simplifier le résultat que tu as trouvé.
tu veux dire me servir de ce que je trouve sur (0;) pour simplifier mon résultat..
sur l'axe vettical on a
F/=mgcos
en quoi ça aide?
En quoi ça aide ? Ben tu exprimes ton résultat en fonction de MOINS DE PARAMÈTRES.
Vas-y, combine tes deux derniers résultats et extrait .
Annuler
connectez vous