Inscription / Connexion Nouveau Sujet
Etude d'un microscope
Bonjour,
Besoin d'aide pour cet exercice qui s'énonce par:
Un microscope porte les indications suivantes : Objectif : ×50 ; Oculaire: ×20; Δ=12cm.
1)Donner la signification de chacunes des inscriptions.
2) Determiner le grossissement de ce microscope.
3)Calculer la vergence C2 de l'oculaire et celle C1 de l'objectif.
Ma piste
1) ×50 reprensente la valeur absolue du grandissement de l'objectif : |γ1|=50 ; ×20 represente le grossissement commercial de l'oculaire et Δ est l'intervalle optique.
2) Grossissement du microscope
Je sais néanmoins que G=P×dm où P est la puissance qui vaut P=|y1|.P2
Et dm la distance minimale de vision distincte...
Je doute aussi fort que ce soit le grossissement commercial que l'on demande... Là Gc=Δ/(4*f1*f2)... Mais j'en sais pas trop à propos de f1 et f2 .
Bonjour
Il existe une relation simple entre le grandissement transversal de l'objectif, f'1 et 
. Tu obtiens simplement f'1.
Il existe une relation simple entre le grossissement commercial de l'oculaire, dm et f'2.
dm étant connu, tu as ainsi simplement les deux distances focales.
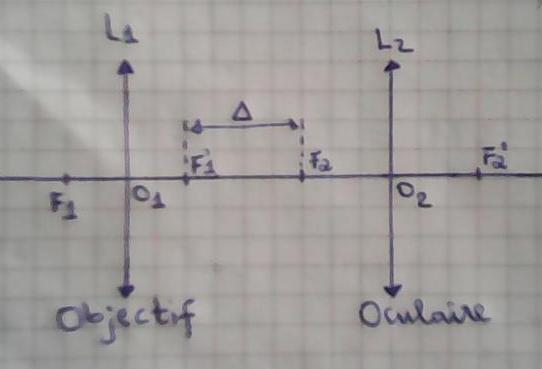
Essaie de faire un schéma de principe du microscope pour bien comprendre. Cela est plus efficace que l'utilisation de formules toutes faites...
Imagine un objet réel AB situé à gauche de F1 de sorte que son image A1B1 par l'objectif soit dans le plan focal objet de l'oculaire : A1 confondu avec F2. Trace quelques rayons issus de B et convergeant en B1. Tu obtiendras alors une relation simple entre 
1, et f'1. Cela te permet d'obtenir la valeur de f'1 et de son inverse C1 puisque 1 et sont fournis par l'énoncé.
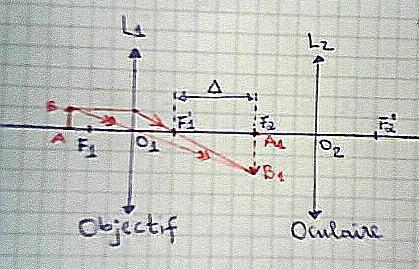
Tu peux compléter le schéma que tu as fait puis le poster sur le forum.
Parfait ! Figure très soignée !
La formule que tu viens de démontrer te fournit donc f'1.
Tu connais la formule du grossissement commercial d'un oculaire fonctionnant comme une loupe. Cela va te fournir f'2 puisque dm=0,25m.
Δ=12cm.
De la première relation, f'1=-12/50=0,24 cm.
La formule du grossissement commercial de l'oculaire est Gc=Pi/4 où Pi=1/f'2
=> Gc=1/4f'2 => f'2=1/4Gc=1/(20*4)=0,0125 cm ?
Attention aux signes et aux unités...
le grandissement étant un rapport de deux longueurs, f'1 et doivent avoir la même unité. Attention aux deux signes "-" !
Le grossissement commercial de l'oculaire est :
dm et f'2 doivent avoir la même unité. Si tu remplaces 25cm par (1/4) de mètre, tu obtiens une distance focale exprimée en mètre, pas en cm !
Okay super.
2) Le grossissement de ce microscope est donc: G=P*dm=|y1|*P2*dm or P2=Pi=1/f'2.
G=|y1|*(1/f'2)*dm=|-50|*(1/1,25)*25=1000.
3)• La vergence de l'oculaire est C2=1/f'2=1/0,0125=80δ;
•Celle de l'objectif est C1=1/f'1=1/0,0024=416,67δ.
.
Annuler
connectez vous