Inscription / Connexion Nouveau Sujet
Étalonnage d'un ressort
Bonsoir
J'aurais besoin d'aide pour cet exercice
On relève la longueur L d'un ressort à spires jointives en fonction des forces appliquées :
| F(N) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| L(cm) | 12,5 | 12,5 | 12,6 | 13,2 | 13,7 | 14,3 | 14,6 |
1/ Tracer la courbe donnant les variations de F en fonction de l'allongement(a).
2/ Donner l' équation de la courbe obtenue .
3/ Comparer cette courbe avec celle d'un ressort à spires non jointives .
Conclure .
4/ Un tel ressort peut-il servir pour fabriquer un dynamometre ?
Dans quel domaine d'intensité de force peut-il servir ?
On me demande de tracer la courbe en fonction de l'allongement et j'ai la longueur.Comment faire pour avoir l'allongement ?
Merci d'avance

Bonjour,
L'allongement est dû à une force. Quand il n'y a pas de force il n'y a pas d'allongement.
Donc... l'allongement est égal à la longueur diminuée de la longueur à vide.
Ici, l'allongement (en centimètres) est égal à L(cm) - 12,5

Pour tracer la courbe, l'énoncé te donne les coordonnées de 7 points.
Puisque l'on te demande "les variations de F en fonction de l'allongement", il faut placer :
. en abscisse les valeurs de l'allongement (pas une seule valeur, mais les 7 valeurs ! )
. en ordonnée les valeurs de la tension F
Puis, faire passer au mieux une courbe par ces 7 points.

Merci Coll
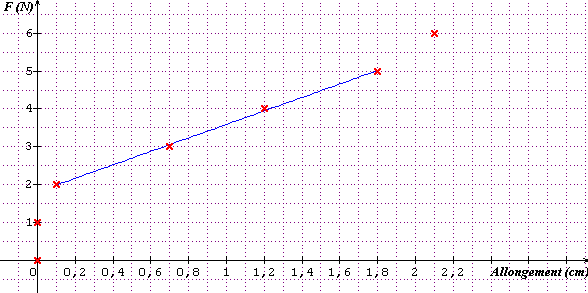
Voici les valeurs de la courbe que je devrai représenter en prenant comme échelle :1cm ---->1N ; 1cm ---->0,2 cm
| F(N) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| a(cm) | 0 | 0 | 0,1 | 0,7 | 1,2 | 1,8 | 2,1 |
Si c'est bon le reste est de savoir où je place le point 0
Merci

Tu ne sais pas si l'équation que tu proposes est correcte.
Il est simple de la vérifier : tu calcules F par ton équation pour les différentes valeurs de a : tu dois retrouver (à très peu près) les valeurs de l'énoncé.
Conclusion : je pense que ton équation est fausse.

Je t'ai expliqué comment faire pour le savoir...
Mais on voit, au premier coup d'il, que ce ne peut être cela. L'ordonnée à l'origine n'est pas négative...
Tu as appris comment déterminer l'équation d'une droite quand on en connaît deux points.
Par exemple par le calcul du coefficient directeur puis de l'ordonnée à l'origine.
Tu peux aussi écrire que tu connais la forme générale de l'équation d'une droite :
En écrivant par exemple que la droite passe par les deux points (0,1 ; 2) et (1,8 ; 5) les coefficients inconnus, a et b, sont tels qu'ils sont solution des deux équations à deux inconnues (que tu as appris à résoudre au collège, en troisième) :

Je n'avais pas vu ta réponse de 11 h 20
L'ordonnée à l'origine est acceptable. Mais le coefficient directeur est toujours faux.

Oui j'ai appris cette résolution
Je sais que y= ax +b
a= △F/△a
a= 5-2/(1,8-0,1)-2
On a a= k= 176,47 ?
L'allongement est exprimé en centimètres ; et il ne faut pas chercher à l'exprimer en mètre.
a  1,764 (N.cm-1)
1,764 (N.cm-1)
b  1,823 (N)
1,823 (N)
On peut se contenter de F(N)  1,76
1,76 a(cm) + 1,82
a(cm) + 1,82

Bien sûr.
Et en remplaçant x par 0,1 cm tu trouves F  1,76
1,76  0,1 + 1,82 = 1,996 N
0,1 + 1,82 = 1,996 N
à comparer à 2 N
Pas mal, non ?

Pour la question 3/ ,d'abord comment expliquez-vous un ressort à spires jointives et non jointives.
Merci Coll
Comment est la courbe pour un ressort à spires non jointives ? (il y a de nombreux exemples dans le forum...)

Exact.
Si bien que pour les petits allongements il y a proportionnalité entre ces allongements et la force appliquée (fonction linéaire et non pas fonction affine comme pour le segment de droite de mon graphique).

Peut-être.
J'aurais tendance à être plus prudent et à limiter l'usage de ce ressort à l'intervalle de 2 newtons à 5 newtons (c'est-à-dire le segment bleu de mon graphique).

C'est vrai
Merci Coll
Je profite, si vous me permettrez, de poser une question:
Dans quel cas qu'on doit multiplier la raideur K par g (intensité du champ de pesanteur) pour avoir le coefficient directeur a ?
Merci