Inscription / Connexion Nouveau Sujet
equilibre d'un solide soumis à l'action de trois forces non para
Bonsoir ,s'ils vous plait j'ai besoin d'un coup de main pour resoudre cet exercice rapidement je suis bloqué au niveau de la 2eme question.Merci d'avance.
Exercice:Un corps A de poids p=3N repose sans frottement sur un plan incliné d'angle alpha=30° avec l'horizontale.La reaction du plan sur le corps A est perpendiculaire au plan.Le corps est maintenant sur le plan incliné par l'intermedieure d'un ressort faisant un angle beta avec la ligne du plus grande pente.
avec la ligne du plus grande pente.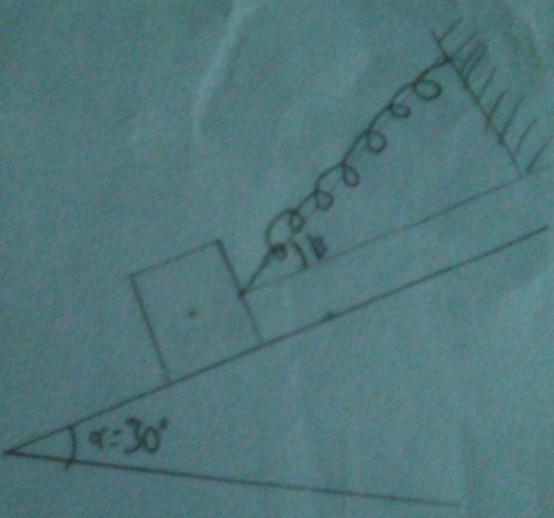 .
.
1)Faire les bilan des forces.
2)En deduire l'intensité de la force T exercé par le ressort sur le corps A en fonction de l'angle 
3)Calculer T lorsque  =0°;
=0°; =30°
=30° =60° et en deduire dans chaque cas l'allongement du ressort si la raideur K=50N/m.
=60° et en deduire dans chaque cas l'allongement du ressort si la raideur K=50N/m.
Bonsoir,
1) Bilan des forces
Trois forces s'exercent sur le corps A :
a) Son poids , force verticale dirigée vers le bas et d'intensité 3N
b) La réaction du plan, force perpendiculaire au plan dirigée vers le haut et d'intensité inconnue.
c) La force exercée par le ressort dont la direction fait un angle
 avec la ligne de plus grande pente du plan et d'intensité inconnue.
avec la ligne de plus grande pente du plan et d'intensité inconnue.
2) Le corps A est en équilibre ce qui implique que la somme vectorielle des forces qui s'exerce sur A est nulle :
En projetant cette relation vectorielle sur un axe Ox parallèle à la ligne de plus grande pente du plan tu auras la réponse à la question 2
3) Rappel : L'intensité de la force T est proportionelle à l'allongement  L du ressort : T = K*
L du ressort : T = K* L
L
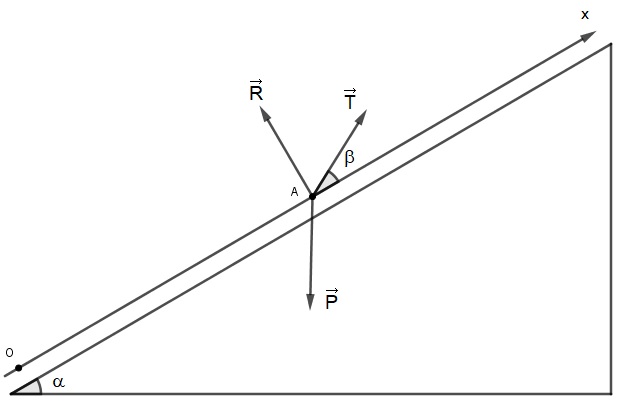
Decomposition des forces:
P(-px;-py)+R(0;R)+T(tx;ty)=0.
Projection sur l'axe x'x:
-px=-p.sin 
Rx=0
tx=t.cos
Sur l'axe y'y:
-py=-p.cos
Ry=R
ty=t.sin .
.
Est ce bien ça?
Bonjour,
Oui, c'est exact sauf en ce qui concerne ty, mais il s'agit probablement d'une étourderie.
De plus cette petite erreur n'a pas de conséquences puisque tu n'as besoin que de la projection sur Ox (et pas de la projection sur Oy) pour répondre à la question posée.
Il te reste à terminer la question 2 et traiter la question 3

 au niveau de la 2eme question .
au niveau de la 2eme question .

