Inscription / Connexion Nouveau Sujet
Équilibre d'un solide soumis à des forces non parallèles
Bonsoir
J'aurais besoin d'aide pour cet exercice:
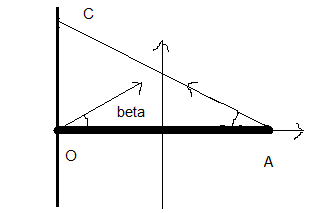
Une étagère est constituée par une planche homogène de masse m= 2kg et de longueur OA =l=20 cm .Elle est sur un mur vertical par une articulation d'axe △ horizontal.La planche est retenue par un câble AC.On donne:
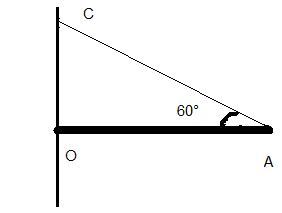
OAC= 60˚; g= 9,8 N/kg
Déterminer ,à l'équilibre la tension du fil AC et la réaction du mur en O.
Ma réponse:
R= Tcos /cos
/cos ?
?
T= P-Rsin /sin
/sin ?
?
Si c'est vrai ,que vaut angle  ?
?
Merci d'avance
Bonsoir,
il représente quoi l'angle  ? et l'angle
? et l'angle 
Si  est l'angle OCA, alors il suffit faire 180°-90°-60°=30° (la somme des angles d'un triangle vaut 180°
est l'angle OCA, alors il suffit faire 180°-90°-60°=30° (la somme des angles d'un triangle vaut 180°
Si  est l'angle OCM (où M est le milieu de OA), alors tu calcule la longueur OC, puis tu en déduit l'angle
est l'angle OCM (où M est le milieu de OA), alors tu calcule la longueur OC, puis tu en déduit l'angle  par trigonométrie dans le triangle OCM
par trigonométrie dans le triangle OCM
Sinon, pourrais tu expliquer ta démarche, ce serait plus simple pour vérifier si c'est correct et t'aider à interpréter ton  .
.
Bonne soirée
Sandro
Tu as 3 inconnues dans ton système (R, T et  ) : tu as donc besoin de 3 équations les liant pour pouvoir toutes les trouver. Hors tu n'en obtient que 2 en projetant sur les axes.
) : tu as donc besoin de 3 équations les liant pour pouvoir toutes les trouver. Hors tu n'en obtient que 2 en projetant sur les axes.
Il te manque donc une équation. Or tu n'as aucun lien géométrique entre R, T et  : c'est donc une équation physique qui manque. En effet, en appliquant le principe d'équilibre des forces à l'étagère, tu traduit le fait que le centre de gravité de l'étagère ne bouge pas. Il reste à traduire le fait que l'étagère ne tourne pas (en vocabulaire courant : qu'elle ne bascule pas). Et là, je vois mal comment mettre ça en équation au niveau seconde (après je ne connais pas non plus les programmes actuels).
: c'est donc une équation physique qui manque. En effet, en appliquant le principe d'équilibre des forces à l'étagère, tu traduit le fait que le centre de gravité de l'étagère ne bouge pas. Il reste à traduire le fait que l'étagère ne tourne pas (en vocabulaire courant : qu'elle ne bascule pas). Et là, je vois mal comment mettre ça en équation au niveau seconde (après je ne connais pas non plus les programmes actuels).
La seule solution que je vois qui est à peu près abordable est le principe du bras de levier : le poids s'applique au milieu M de OA (le centre de gravité) alors que la traction du fil s'applique en A, c'est à dire 2 fois plus loin du pivot O et a donc un bras de levier 2 fois plus important. Par conséquent la traction du fil (enfin, sa composante perpendiculaire à (OA), donc sa composante verticale) a 2 fois plus d'effet sur la rotation que le poids. (R n'intervient pas car appliqué au point pivot)
Donc (où
est la partie verticale de
) donc -m.g+2.T.sin(
 )=0 donc
)=0 donc
Si on remplace  par sa valeur (60°), on obtient
par sa valeur (60°), on obtient
Ensuite, si tu projette sur les axes, tu obtiens tes équation : il me semble que la 1ère est juste, et qu'à la seconde, tu as oublié des parenthèses : je crois que c'est plutôt )
Tu as donc déjà T et il te reste 2 équations (les 2 obtenues par projections) et 2 inconues (R et  )
)
Je te conseille de ne pas chercher à calculer  (dur et inutile), mais de calculer directement R. Astuce : isole cos(
(dur et inutile), mais de calculer directement R. Astuce : isole cos( ) et sin(
) et sin( ) puis utilise le fait que cos(
) puis utilise le fait que cos( )²+sin(
)²+sin( )²=1
)²=1
En espérant avoir pu t'aider
Sandro
PS : j'espère ne pas avoir fait d'erreurs de calculs, je commence à être bien fatigué
PS2 : essaye de mettre le plus d'infos possibles sur les schémas :
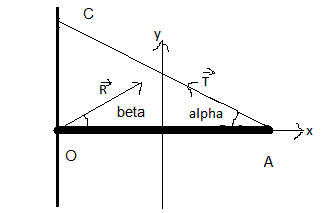
Et à décider des signes des angles et des lettres : positifs ou relatifs : moi j'ai choisit de prendre à la fois les angles, R et T comme positifs (mais c'est un choix libre, il faut juste préciser)
Désolé plutôt =P/ sin
On avait :
-Tcos +Rcos
+Rcos =0 et
=0 et
Tsin -P+Rsin
-P+Rsin =0
=0
En appliquant votre conseil on a :
(1) R= 22,63 N
(2) T=P-Rsin /sin
/sin ?
?
Mais sin reste inconnu
reste inconnu
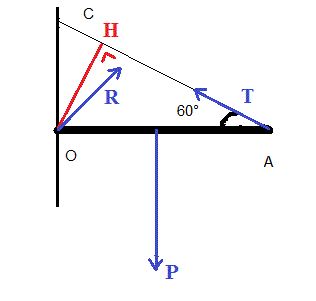
Somme des moments des forces sur la planche autour de O = 0
P*OA/2 - T * OH = 0
P*OA/2 - T * OA.sin(60°) = 0
T = mg/(2.sin(60°)) = 2 * 9,8/V3 = 11,3 N
Rx = -T * cos(60°) = 5,65 N
Ry = P - T.sin(60°) = 9,81 N
R = V(5,65²+9,81)² = 11,3 N
Ry = Rx.tg(Beta)
Beta = 60°
-----
Sauf distraction.