Inscription / Connexion Nouveau Sujet
Équilibre d'un solide mobile autour d'un axe fixe
Bonsoir
J'aurais besoin d'aide pour cet exercice:
Deux enfants de masse mA et mB sont assis aux extrémités A et B d'une planche homogène servant de balançoire. La masse de la planche est de 15 kg et sa longueur de 2 m .La planche repose sur un rondin de b bois servant d'axe horizontal situé à la distance x= 0,8 m de A.
1.À l'équilibre la balançoire est horizontale .Calculer mA et mB sachant que mB= 8/13.mA.
2.Calculer la réaction de l'axe .
3.Un 3ème enfant de masse mC= 20kg joue à déséquilibrer la balance ; il se place à la distance Y= 0,2 m de B sur la planche.
a. Montrer qu'en déplaçant le rondin dans un sens et sur une distance que l'on détermine on peut rétablir l'équilibre .
b. Que devient la réaction de l'axe.
Mes réponses:
On a projeté sur les axes→ mA= -m*13/8 = -24,375 kg et mB= 15kg
Est-il just ?
Merci d'avance
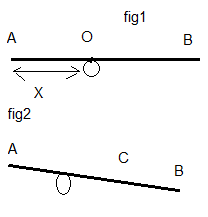
Voici les figures:
tu t'es trompé dans le calcul des moments en O
en posant m = 15kg (masse de la planche)
0.8 mA g = 0.2 m g + 1.2 mB g
donc
0.8 13/8 mB - 1.2 mB = 0.2 m
0.1 mB = 0.2 m
...
sauf erreur car il est tard 
1)
mA * x - mB * (L - x) - mp * (L/2 - x) = 0
mA * 0,8 - mB * (2 - 0,8) - 15 * (1 - 0,8) = 0
0,8.mA - 1,2.mB - 3 = 0
Avec mB = 8/13 mA -->
0,8.mA - 1,2 * (8/13).mA = 3
mA = 48,75 kg
mB = 8/13 * 47,75 = 30 kg
-----
2)
R = (mA + mB + mp)*g = ... N (vertical vers le haut)
-----
3)
a)
mA * x - mB * (L - x) - mp * (L/2 - x) - mC * (L - x - 0,2) = 0
48,75.x - 30.(2 - x) - 15 * (1 - x) - 20.(2 - x - 0,2) = 0
113,75 x = 111
x = 111/113,75 = 0,9758 m (arrondi)
b)
R = (mA + mB + mp + mC)*g = ... N (vertical vers le haut)
-----
Recopier sans comprendre est inutile.
Sauf distraction. 



