Inscription / Connexion Nouveau Sujet
Equilibre d'un solide dans un plan incliné (rdm)
bonjour à touse et à toute.
Voila mon petit problem.
Une sphère est posée sur un plan incliné a 60° par rapport a l'horizontale.
Sachant que le poids de la sphère est de 30 N (Newton),trouver, par calcul et graphiquement la force a appliquer, parallelement au plan incliné, a la sphère, pour la maintenir en équilibre.
Voila, si quelqu'un pouvez m'aider.....
Merci d'avance
Salut !
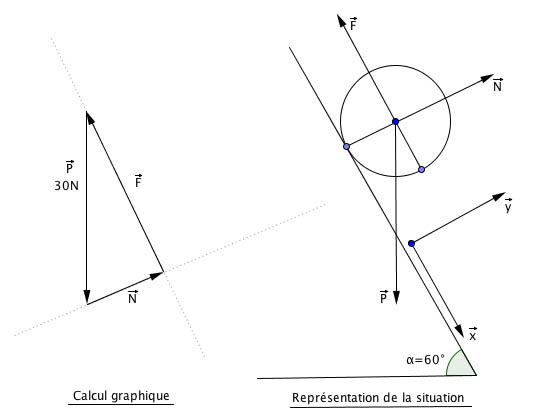
Alors déjà, pour résoudre ce genre de problème, la première chose à faire est de faire un schéma, si c'est pas déjà fait, et d'y représenter les différentes forces appliquées à la sphère : Le poids (\vec{P},Norme : 30N, Direction : Verticale, Sens : vers le bas), la réaction normale au support (\vec{N} ,Norme : ?, Direction : Normale au support, Sens : Vers le haut) et la force qui empêche le déplacement de la sphère (\vec{F} ,Norme : ?, Direction : Parallèle au support, Sens : Opposé au déplacement).
La deuxième chose à faire, c'est de créer un repère d'axe, je te conseille de l'orienter dans la même direction que la surface (Voir mon schéma)
Et enfin, tu énonces la 1ère loi de Newton, à savoir , puis, faire les (la) projection sur un axe bien choisi
. Puisque la force à appliquer est parallèle à la surface, elle n'aura une composante que sur l'axe , la seule chose à faire est donc de projeter sur l'axe
. Tu obtiens donc
, soit
(Tu devrais trouver environ 25N) . Ca c'était pour la résolution algébrique
Maintenant, pour la méthode graphique (Voir schéma), la première chose est de définir une échelle, genre . Ensuite, tu représentes la force dont tu connais tout (Norme, sens, direction), à savoir le poids, avec l'échelle que tu as défini. Ensuite, tu vas tracer une droite ayant la même direction que la réaction du support, à l'extrémité du vecteur représentant le poids. Tu fais la même chose pour le vecteur qui représente la force appliquée à la bille (J'ai représenté ces droites en pointillé sur le schéma). Ensuite, avec l'intersection de ces deux droites, tu peux déterminer exactement (A la précision du tracé près) la norme de
en utilisant l'échelle que tu as défini au début du tracé. Tu devrais retrouver quelque chose de semblable à ce que tu avais trouvé avec le calcul algébrique
ça me rassure.
j'avais bien commencer. je m'étais juste trompé dans la formule, j'avais mis sin :s
merci pour ton aide en tout les cas
j'aurais d'autre petit problem à résoudre a nouveau un peu plutard des que je mis serai penché deçu
merci bien
Annuler
connectez vous