Inscription / Connexion Nouveau Sujet
Equation horaire mouvement rectiligne uniforme
Bonjour tout le monde
J'ai du mal à comprendre les équations horaires , comment ça fonctionne. J'ai un exercice
Exercice
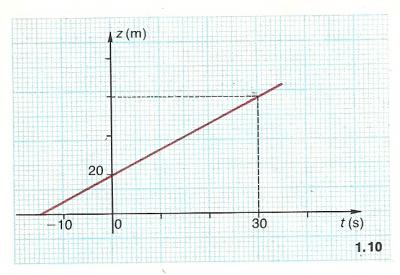
Un mobile se déplace sur un axe z'z. On a représenté graphiquement la fonction t  z(t).
z(t).
1/ Déterminer la position du mobile à l'origine des dates.
2/ A quelle date le mobile passe-t-il par la position origine z = 0?
3/ Déterminer l'équation horaire du mouvement. Quelle est la nature de ce mouvement? Déterminer la vitesse du mobile en chaque point de la trajectoire rectiligne.
Pour le 1/ à t = 0 , x = 20 m
2/ Moi j'aurais dit -15 s mais dans le corrigé c'est écrit -10 s
3/ Je ne sais pas comment faire
Merci d'avance
Bonjour Sid.
On ne peut pas vous guider sans voir la représentation graphique.
Merci de la poster.
A plus.
Bonjour Sid07
Bonjour picard 
1) D'accord. Pour t = 0 s la position est z = 20 m
2) C'est toi qui as raison et le corrigé qui a tort
C'est bien pour t = -15 s que z = 0 m
3) L'équation horaire, c'est simplement l'équation de cette droite z(t) = ...
Cela permet de connaître, dans le domaine de définition (par exemple il semble que ce soit t  -15 s ou peut-être -15 s
-15 s ou peut-être -15 s  t
t  35 s) pour chaque valeur de t quelle est la position z
35 s) pour chaque valeur de t quelle est la position z
Tu sais déterminer l'équation d'une droite (fonction affine...)
Quelle est la nature du mouvement ?
Relis le titre du topic !
Quelle est la vitesse en chaque point, sachant que le mouvement est uniforme et que tu as déterminé l'équation de la droite ou équation horaire de ce mouvement ? (n'oublie pas l'unité ! )

Pour les fonctions affines l'axe des abscisses c'est les variables et l'axe des ordonnées c'est les images. Mais ici c'est l'inverse non ?
Moi j'aurais fait
z(20) = 20v+x0
20v + x0 = 0 1)
z(60) = 60v + x0
60v + x0 = 30 2)
Je résous le système , je trouve v = 3/4 et x0 = -15
donc z(t) = 3/4 t -15
Et j'ai l'impression que c'est juste , corrigez moi si j'ai fait une erreur ^^
Merci de m'aider
La variable est le temps t (en secondes) et en fonction du temps on déduit la position z (en mètres).
Une valeur de t est un antécédent
Il lui correspond une image qui est une valeur de z
La fonction est notée z(t), donc ce n'est pas "l'inverse" comme tu l'écris.
Tu peux déterminer l'équation de la droite en en prenant deux points.
Je te propose les deux points extrêmes du segment
t = -15 s
z = 0 m
et
t = 30 s
z = 60 m
Les deux points sont donc (-15 , 0) et (30 , 60)
En effet, tu n'as pas écrit un système correct et donc l'équation trouvée est fausse.

J'ai trouvé comme équation horaire z = 4/3t + 20 .
Il y a quelque chose qui me chiffonne, je ne sais pas si c'est le corrigé qui est erroné car il trouve z = 2t , je me demande si on peut transformer une équation affine en une équation linéaire en translatant la courbe de la fonction affine et passant maintenant par l'origine du repère .Et je pense bien que c'est le corrigé qui est erroné.
A partir de l'équation horaire que j'ai trouvé, je peux en déduire que v = 4/3 m/s
v  1,34 m/s
1,34 m/s
Re-bonjour Sid, salut Coll.
Votre équation horaire est correcte.
Non, z = 2 t ne peut pas coller même en envisageant un changement d'origine ; à la limite, on pourrait avoir z' = 4/3 t, en décalant l'origine de l'axe vertical, mais le coefficient directeur restera égal à 4/3.
D'accord pour la vitesse v = 4/3 m/s.
Au revoir