En réflechissant un peu j'ai réussi à trouver une solution égale à environ (avec tous les arrondis..) 12h21 (et 13 secondes ? :p) et distant de 7km à peu près.
Je ne garantis absolument pas le résultat et je n'ai malheureusement pas le temps de développer mon raisonement étant donné que j'ai encore quelques révisions à faire en vue du bac...

En bref, pour t'aider à commencer, j'ai pris A comme origine du repère et placé B tel que l'angle OAB ait pour mesure 45° et AB = 20km. Après avec quelques considérations géométriques on peut, je pense, arriver à un résultat.

Bon courage.

O étant le point désignant l'Ouest sur ton dessin lorsque je parle de l'angle OAB

oui mais ça ne va pas , ils me disent : à quelle heure B sera à l'ouest de A? mais B est déjà à l'ouest...puis ils vont à la même vitesse , d'aprçs ton dessin , B se retrouverait en A , et A un peu plus haut sur l'axe des y , comme ils vont tous les 2 à 20km/h , ils seraient tjs distants de 20km...

salut
oh on dirait mon métier (croisement d'avion ds le ciel )
c'est exactement pareil
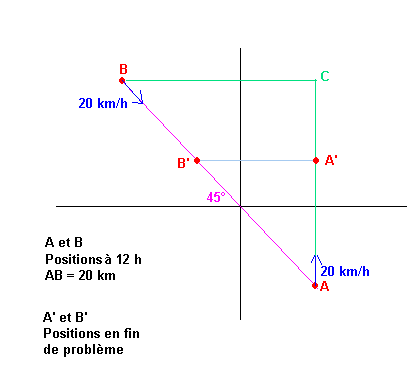
donc si on prend le repère du squal donc A origine situé en haut à gauche à 45° et 20km de A
donc les coordonnées de A (0;0) et celles de B sont (20V2/2;20V2/2) soit B(10V2;10V2)
donc au bout d'un temps t le point A est monté sur Ay pour devenir A' dont les coordonnées sont A'(0;vt) et B est devenu B' en avançant d'une distance BB'=vt  vers A sur l'axe AB et donc les coordonnées de B' sont en abscisse (20-vt)V2/2 et en ordonnée pareil
donc toi tu cherches t pour que les deux ordonnées soient les mm
comme ça B' est dans le plein ouest de A' et c ce qu'on te demende qd on dit dans l'ouest
donc il faut résoudre vt=(20-vt)V2/2 et tu connais v=20km/h
bonne chance

Bonjour,
le problème vient peut etre du faite que B va dans le sens inverse de celui dessiné!
tu poses A a l'ouest de B et ton problème de dessin disparait

Salut,
Plaçons-nous dans un repère(O,,) l'unité étant le km.
Notons t le temps (en heures) qui s'est écoulé à partir de midi.
Notons A(t) le point qui représente le bateau A.
Notons B(t) le point qui représente le bateau B.

Pout t=0 (c'est-à-dire à midi), je suppose que A(0) est à l'origine O du repère ie A(0)(0,0). A ce moment-là, et si j'ai bien compris la situation, on a B(0) soit B(0)

A(t) se déplace vers le nord à la vitesse de 20 km/h donc A(t) a pour coordonnées A(t)(0,20t)

B(t) se déplace, si j'ai bien compris, suivant le vecteur -.
Donc les coordonnées de B(t) sont avec z(t) une fonction qui reste à déterminer et z(t)>0

La vitesse du bateau B est 20 km/h donc B(0)B(t)=20t
Or B(0)B(t)=donc

On a donc B(t)
soit B(t)
et on a aussi A(t) (0,20t)

Le point B(t) sera à l'ouest du point A(t) quand les deux points auront la même ordonnée.

Il faut donc résoudre
On trouve soit t0,414... h
Ce qui donne environ 25 minutes

Bye.

tu as utilisé les équations horaires ici non?

je comprends pas trop avec ta fonction z(t) , et surtout je comprends rien sur ceci : si B se déplace en ligne droite , il arrivera automatiquement en A en 1 heure et surtout il est déjà à l'ouest de A

je ne sais pas ce que tu entends précisément par "équations horaires" ...

en fait quand on dit que B sera à l'est de A ça suppose que la droite (ab) sera parallèle à l'axe ouest-est...

oui, c'est ça.

je crois que c'est les équations horaires que tu as utilisé mais je vais essayer de reformuler le problème :

le point A , a pour équations horaires x = f(t) , y = g(t) , et  B , x=f(t) , y=g(t) , ici :

A , 0 = f(0) , 0 = g(0)
B , -102 = f(0) , 102 = g(0)

et en fait je dois trouver  quand A , g(t) = B , g(t) par rapport au temps , c'est à partir d'ici que j'ai dû mal à décrire un raisonnement grâce aux équations horaires...

quelqu'un pour m'éclairer svp?

personne ?

AC = AB.cos(45°) = 20/V2 km (avec v pour racine carrée).

Composante vers le Nord de l'avancée de A: d1 = 20 t  (avec d1 en km et t en heures)

Composante vers le Sud de l'avancée de A: d1 = 20.sin(45°).t

Le bateaux se rapprochent (dans la direction Nord-Sud) de: 20 t + 20.sin(45°).t

Ils seront sur la même ligne (Ouest-Est) lorsque: 20 t + 20.sin(45°).t =  20/V2

20 t + 20.sin(45°).t =  20/V2

t + sin(45°).t =  1/V2

t.(1 + (1/V2)) = 1/V2

t.(1+V2) = 1

t = 1/(1+V2) = 0,41421... heure = 24 min 51 secondes et des poussières.

Le navire B sera à l'ouest de A 12h 24min et 51 secondes (et des poussières).
-----
Le bateau A aura parcouru (depuis midi) la distance AA' = 20 * 0,41421 = 8,2842 km

On a alors= A'B'/BC = AA'/AC  (par triangles de même forme).

Avec: BC = AC = 20/V2 --->

distance entre les bateaux A'B'= 8,2842 km
-----
Sauf distraction, vérifie les calculs.  

JP , je te remercie bcp de tes schémas , accompagnés d'explications détaillées , mais je dois utiliser les équations horaires pour résoudre ce problème , et pour simplifier je pensais choisir A comme originie , et dire que AB = 20km , là je suis totalement embrouillé car tu utilises une méthode que je ne connais pas , avec les équations horaires on bosse avec les coordonnées de points en fonction du temps , sur ton schéma tu donnes pas de coordonnées à a ou à b , enfin pas grave , j'abandonne , il me soule cet exercice , merci :'(

en fait je comprends pas ta méthode , tu dis qu'ils seront sur la même ligne quand la somme de leurs équations horaires sera égale à AC , pourquoi? je comprends pas en fait ce que vient faire AC la dedans .

et j'ai un peu de mal aussi avec ceci :


Composante vers le Sud de l'avancée de A: d1 = 20.sin(45°).t

je crois que tu as voulu dire B à la place de A , le 20 c'est pour la vitesse , le t c'est pour le temps , et le sin45° pour la déplacement en diagonale?

enfin là le AC me perturbe bcp , je ne sais vraiment pas comment tu as  décidé qu'il fallait se servir de AC , quelle règle as tu suivi...

à en fait je crois avoir compris , tu as pris comme référence de déplacement des points le segment AC , et sur AC , le point A se déplace effectivement par 20t , et tu as dit que le déplacement du point B était 20.sin(45°).t par rapport au segment AC , voilà je pense que c'est ceci , maintenant le seul dernier hic c'est : pourquoi le déplacement de A + le déplacement de A devrait être égal à AC ?
quelle est cette méthode , j'ai jamais vu çà...

pourquoi le déplacement de A + le déplacement de B devrait être égal à AC ?

petite rectification

Salut Apprenti,

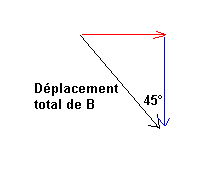
Si tu décomposes le déplacement total de B en 2 composantes (une en rouge sur le dessin, correspondant au sens OUEST vers EST et l'autre en bleu le dessin, correspondant au sens NORD vers SUD.)

La longueur en bleu = la longueur en noir * cos(45°)

La longueur en bleu = la longueur en noir / V2  (avec V pour racine carrée).

Le déplacement total de B après un temps t est donné par 20 km/h * temps (avec le temps en heure).

La composante bleue est donnée par  20 km/h * temps /V2

soit (20/V2).t
---
Pendant le même temps "t", le bateau A va vers le nord d'une distance 20.t
---

Donc la distance (dans la direction Nord-Sud) qui sépare les 2 bateaux diminue avec le temps comme: (20/V2).t + 20.t
---

Or à midi, les 2 bateaux sont distants de 20 km, on peut de nouveau décomposer cette distance en 2 composantes, une Nord-Sud et l'autre Ouest-Est.

On a la distance N-S = 20.cos(45°) = 20/V2 km
---

Lorsque les 2 bateaux auront ENSEMBLE parcourut une composante N-S de 20/V2 km, ils seront sur la même droite OUEST-EST.

Cela se traduit par: 20/V2 = (20/V2).t + 20.t

On peut alors tirer de là, le temps t qu'il faut pour que les bateau xsoit alignés dans la direction Ouest-Est.

20/V2 = (20/V2).t + 20.t

20/V2 = t.[(20/V2). + 20]

1/V2 = t.[(1/V2). + 1]

1/V2 = t.(1 + V2)/V2

1 = t.(1 + V2)

t = 1/(1+V2) heure

t = 0,41421 heure = 24 minutes 51 secondes et des poussières.
-----
Sauf distraction.