Niveau première

Énergie potentielle et énergie mécanique

Posté par
Barham 09-01-20 à 20:43

Bonsoir j'arrive pas à terminer mon exo aidez moi svp j'ai des difficultés avec la dernière question.
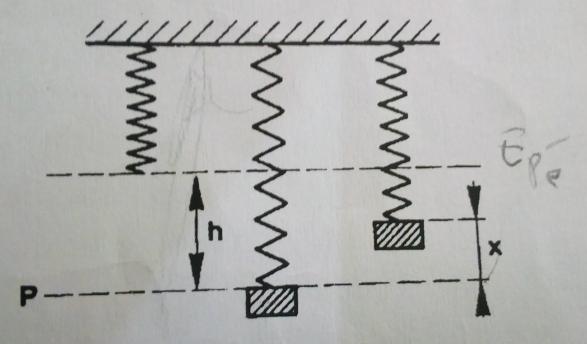
Une masse m est suspendue à l'extrémité inférieure d'un ressort vertical de masse négligeable dont l'autre extrémité est fixe . En étirant le ressort on amène son extrémité inférieure dans un plan horizontal P qui sera pris comme plan de référence d'altitude 0
Puis on abandonne la masse m . L'extrémité du ressort effectue alors des oscillations verticales . On représente par x l'altitude de l'extrémité du ressort à l'instant t et par h son altitude quand le ressort est au repos
L'énergie potentielle du système masse m Terre sera prise égale 0 pour x= 0
1) exprimer l'énergie mécanique du système au début du mouvement et à l'instant t. En déduire une relation entre la vitesse v de la masse m à l'instant t et la variable de position x
2/ pour quelles valeurs de x observe t on une vitesse nulle de la masse m?
3/ Montrer que l'énergie cinétique du système est maximale quand la masse m passe à sa position d'équilibre.
Données : m= 0,1kg
h= 0,15m
K= 10N/m

Énergie potentielle et énergie mécanique

Posté par re : Énergie potentielle et énergie mécanique 09-01-20 à 22:08

Hello

Partager les résultats que tu obtiens aux questions 1/ et 2/ nous aiderait à t'aider pour la question 3/

Pour cette question, je te recommande, une fois rappelée l'équation traduisant la conservation de l'énergie mécanique (Ep + Ec = constante) d'exprimer la vitesse comme une fonction de l'allongement x. Puis de démontrer que cette fonction passe par un maximum pour x = 0

Posté par re : Énergie potentielle et énergie mécanique 09-01-20 à 22:17

Si j'egalise l'énergie mécanique en x et l'énergie mécanique à l'état d'équilibre j'aurais Ec(x)= mgh-mgx +1/2(h-x)²
Dois je calculer ce résultat ??

Posté par re : Énergie potentielle et énergie mécanique 09-01-20 à 22:38

En 1/ 0 est l'origine des altitude pour x= 0 et l'état du ressort ni allongé ni comprimé coïncide avec état de référence de l'énergie potentielle élastique
•Em au début du mvnt
Em= 1/2kh²
• Em à l'instant t
Em= mgx-1/2k(h-x)²+1/2mv²
Pour la déduction de la relation entre v et x
V²= -k/m(x²) -2((-kh+mg)/m)x
Pour le calcul de x
On a x=0 ou x= 0,1 m

Posté par re : Énergie potentielle et énergie mécanique 11-01-20 à 06:37

Hello

Petite coquille, x = 0 est l'état de référence de l'énergie potentielle de pesanteur

$Em = Cste = \frac{1}{2}kh^2 = mgx + \frac{1}{2}k(h-x)^2 + Ec$

(autre petite coquille dans le signe de l'Ep élastique, mais tu te "récupères" derrière)
Donc

$Ec =  \frac{1}{2}mv^2 = x(kh - mg - \frac{1}{2}kx)$

Donc v(x) = 0 pour

$x = 0$      ou bien pour     $x = 2(h - \frac{mg}{k})$

3/ $Ec(x) = - \frac{1}{2}kx^2 + x(kh - mg)$

Arrivé là sois tu poses que l'énergie cinétique passe par un extremum pour x tel que $\frac{dEc}{dx} = 0$
Sois tu te "rappelles" qu'une parabole a son sommet en   " $x = -\frac{b}{2a}$ "

Dans les 2 cas tu trouves que la vitesse est maximale pour   $x = h - \frac{mg}{k}$

Ce qui est "rassurant" puisqu'il s'agit bien du milieu entre les 2 positions extrêmes calculées plus haut où la vitesse était nulle

Posté par re : Énergie potentielle et énergie mécanique 11-01-20 à 16:09

N'existe t- il pas une autre méthode ? Je n'ai pas encore vu cette leçon

Posté par re : Énergie potentielle et énergie mécanique 11-01-20 à 18:55

Ok,
Je t'en propose donc une 3eme (passant par une équation bicarrée):

$Ec(x) = - \frac{1}{2}kx^2 + x(kh - mg)$

Soit

$Ec(x) = - \frac{1}{2}k(x^2 + 2(\frac{ mg}{k}-h)x)$

Donc $Ec(x) = - \frac{1}{2}k[(x + \frac{ mg}{k}-h)^2 - (\frac{ mg}{k}-h)^2]$

Donc   $Ec(x) = \frac{1}{2}k[( \frac{ mg}{k}-h)^2- [(x + \frac{ mg}{k}-h)^2]$

Donc Ec(x) est maximale pour x tel que le le 2eme carré de cette différence de carrés est nulle

Soit   $x + \frac{ mg}{k}-h= 0$

Ce qui nous ramène bien à:

$x =  h-\frac{ mg}{k}$

Posté par re : Énergie potentielle et énergie mécanique 12-01-20 à 20:44

Je comprends mieux maintenant merci beaucoup de votre aide . Vos explications me seront vraiment utiles

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau première
46 fiches de physique - chimie en première disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Énergie potentielle et énergie mécanique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique