Inscription / Connexion Nouveau Sujet
énergie potentielle électrostatique
Bonsoir
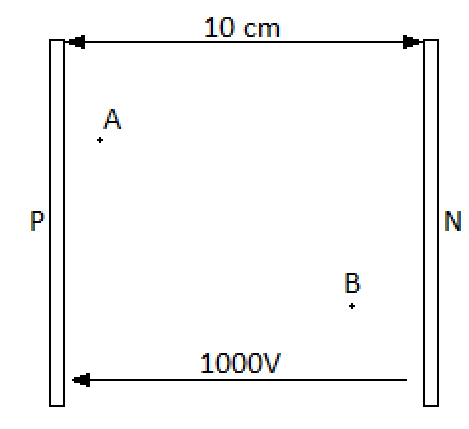
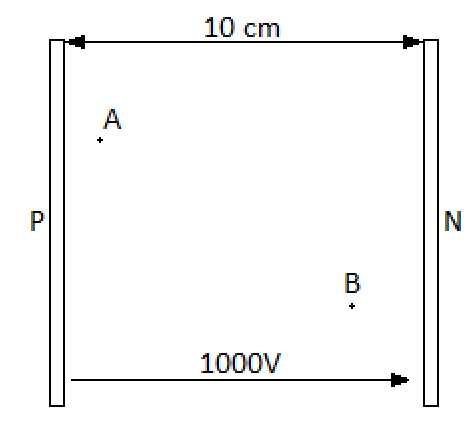
Une différence de potentiel d d p de 10^3 V est maintenue ente deux plaques conductrices identiques , parallèles distantes de 10 cm , une charge q=10^-12 C se déplace entre les plaques d un point A , situé a 1 cm de la plaque positive , a un point B situé a 2cm de la plaque négative.
Calculer
1/ le champ électrostatique entre les deux plaques
E=|V(A)-V(B)|/d
E=10^3/0,1
E=10 V/m
2 / la d d p (V(B)-V(A))=UBA
(V(B)-V(A))=-(V(A)-V(B))
V(B)-V(A)=-10^3
3 l énergie potentiel de la charge q en A , puis B , en prenant comme référence la plaque négative
En A
Epe=qVA
Epe=10^-12×0,1
Epe=10^-13 V
En B
Comme le niveau de référence est la plaque négative
Epe=0
4. Le travail de la force électrostatique s exerçant sur la charge q pour aller de A en B
W(F)= q(VA-VB)
W(F)= 10^-12 × 10^-3
W(F)=10^-15 J
S il vous avez un temps , j aimerais que vous vérifiez mes propositions et si cela n est pas correcte . signaler moi pour que je puisse refaire
Bonjour,
Les définitions et relations entre charge, potentiel, champ électrique et énergie sont correctement utilisées.
En revanche tu commets toujours d'énormes erreurs de calculs.
Exemple à la question 1 ou tu écris que 10³ / 0,1 = 10 
Rappel : 10a / 10b = 10(a-b)
C'est, en effet 104 V/m
103 / 10-1 = 10(3-(-1)) = 104
Ou bien (en plus simple) : Diviser par 0,1 revient à multiplier par 10
103 / 10-1 = 103 x 10 = 104
Non.
Lis l'énoncé
Le point A n'est pas situé sur la plaque P électrisée positivement.
Le point B n'est pas sur la plaque N électrisée négativement
La tension entre les plaques qui vaut 103 volts n'est pas égale à V(A) - V(B)
Le champ électrique que tu as calculé à la question 1 vaut bien 103 / 0,1 = 104 V/m mais il n'est pas égal
à ( V(A) - V(B) ) / d
Attention
J ai voulu écrire si le champ électrique n est paspas egale |V(A)-V(B)|/d
Alors comment il se trouve que nous avons obtenu le même résultat
Par quelle calculer vous avez trouvé que E=10^4 V /m
E = [ V(P)-V(N) ] / d
et pas [ V(A)-V(B) ] / d
A n'est pas en P , B n'est pas en N
V(P) - V(N) = 103 V
d = 0,1m
E = 103 / 0.1 = 104 V/m
Un minimum de rigueur s'impose :
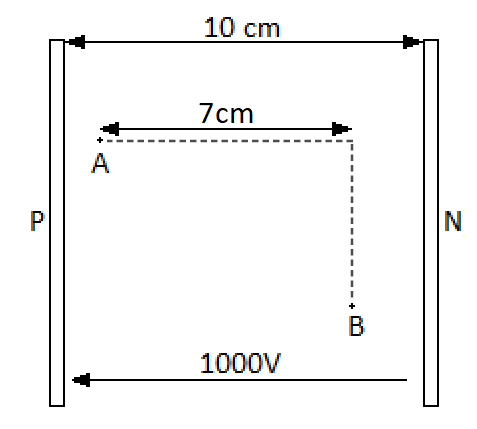
La distance à prendre en compte est en effet de 7cm mais
tu ne peux pas dire comme tu le fais que BA = 7cm !!!!
Mais j ai un souci
Puisque ma méthode n est pas correcte mais ci mon professeur me demandait comment j ai sûre que cette distance est 7 cm
Explique moi comment vous obtenir cela?
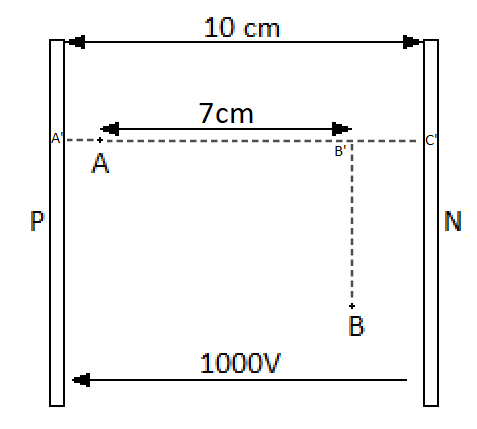
L'énoncé dit :
De A' à C' : 10cm
De A' à A : 1cm
De B' à C' : 2cm
Donc de A à B' : 10 - ( 1 + 2 ) =7cm
Bonjour
V(B)-V(A)=10^4×0,07×cos(vecteur E, vecteur BA)
V(B)-V(A)=10^4×0,07×cos180
V(B)-V(A)=-700 V/m
Je n'insiste plus sur tes incohérences comme par exemple dire que les vecteurs et
forment un angle de 180° (regarde la figure !)
Si tu utilises une autre figure publie là
Le bon résultat est V(B) - V(A) = -700V et pas V/m
Excuse moi
J utilise le même figure que vous
Alors quelle est l angle entre E et BA que je devrais mettre au lieu de 180
Ce n'est pas le vecteur qui forme un angle de 180° avec le vecteur
mais le vecteur
B et B' sont au même potentiel électrique.
Tu peux à la place de calculer V(B) - V(A) calculer V(B') - V(A)
Ok
3/ l énergie potentielle de charge q en A , puis en B, en prenant référence la plaque négative
En A
Epe=qV(A)
Epe=10^-12×0,1
Epe=10^-13 J
En B
Epe =qV(B)
Epe=10^-12×0,02
Epe=2×10^-14 J
Epe=
Non.
Faisons simple.
Entre les plaques existe un champ électrique uniforme de valeur 104 V/m = 102 V/cm
Cela signifie qu'en partant de la plaque négative prise comme référence, à chaque fois que tu te déplaces de 1cm vers l'autre plaque le potentiel augmente de 102 V
Entre la plaque négative (en C') et le point A on se déplace de 9cm
Le potentiel électrique au point A est donc V(A)= 900V
Et l'énergie potentielle correspondante est Epp(A) = qV(A) = 10-12 * 900 = 9.10-10 J
De même au point B
Entre la plaque négative en C' et le point B' on se déplace a 2cm
Le potentiel électrique en B est donc V(B)=200 V
Et l énergie potentielle correspond
Ep(B)=qV(B)=10^-12*200
Ep(B)=2×10^-10 J
3/ le travail de la force électrostatique en A et B
W(F)=q(V(A)-V(B))
W(F)=q(900-200)
W(F)=10^-12×700
W(F)=7×10^-12 J