Inscription / Connexion Nouveau Sujet
énergie potentielle électrostatique
Bonsoir
Ton ami élevé en première D étudié le mouvement d une particule a.
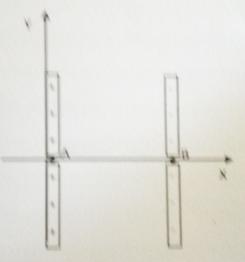
( noyau d hélium He^2+). Cette particule produite par une source radioactive , est émise au voisinage d un point A ( voir figure ci après), la valeur de sa vitesse en A est négligeable devant celle qu elle peut atteindre en B.
Entre les points A et B règne un champ électrostatique uniforme E qui permet l accélération de la particule a.
il se propose de déterminer la différence de potentielle VA-VB
Entre les plaques (VA et VB sont les potentiels respectifs aux point A et B ) . Éprouvant des difficultés , il te sollicite pour l assister .
Données: |e|=1,6 × 10^-19 C ,' ma= 6,70 ×10^-27 kg,
VB=1,00×10^3 km/s( vitesse de la particule a en B)
Le poids et les frottement sont négligeable lors du mouvement
1/ donne la charge sa de la particule a
qa=2×|e|
qa=2×1,6×10^-19
qa=3,2 × 10^-19 C
2/1 établis l expression du travail de la force électrostatique s appliquant sur la particule se déplace entre A et B
2/2 exprime ce travail en fonction de qa , VA et VB
W( F)=qa(VA-VB)
2/3 déduis en l expression de la variation d énergie potentielle électrique entre A et B
∆Ep=-W(F)
3 / dis si l énergie mécanique de la particule a se conserve . justifie ta réponse
Oui l énergie mécanique de la particule se conserve car les forces de frottements sont négligeable
4/1
Exprime la différence de potentiel VA-VB en fonction de VB , ma et qa
w(F)=qa(VA-VB) or VA=0
W(F)= -qaVB
il manque ma dans l expression
Comment faire
4/2 calculer VA-VB
** image supprimée **
Question 4.1 :
4/1
Exprime la différence de potentiel VA-VB en fonction de VB , ma et qa
w(F)=qa(VA-VB) or VA=0
W(F)= -qaVB
il manque ma dans l expression
Comment faire
Utilise la conservation de l'énergie mécanique.
Remarque :
Il me semble que tu notes de la même manière (VA, VB) les potentiels électriques et les vitesses de la particule aux points A et B ce qui , bien entendu engendre des erreurs.
Ok
Appliquons la conservation de l énergie mécanique entre A et B
Em(A)=EC(A)+Ep(A)=ECA+qaV(A)
Em(B)= EC(B)+Ep(B)= EC(B)+qa(VB)
Par d'implication
Em(A)=Em(B)
Ec(A)+qa(VA)=EC(B)+ qaV(B)
EC(A)-EC(B)=qaV(B)-qaV(A)
EC(A)-EC(B)=qa(V(B)-VA) or V(A)=0
1/2 maV^2(A)-1/2 maV^2(B)=-qaV(B)
1/2 ma ( V^2(A)-V^2(B)=-qaV(B)
ma(V^2(A)-V^2(B)=-2qaV(B)
V^2(A)-V^2(B)= -2qaV(B)/ma
Mais quand tu écris :
EC(A)-EC(B)=qa(V(B)-VA) or V(A)=0
Crois tu vraiment que V(A) représente la vitesse au point A ?
Il importe de distinguer V(A) potentiel électrique en A ( en volts )
et VA vitesse de la particule en A ( en m/s)
Je t'ai déjà signalé cette erreur dans mon post du 29-04-19 à 10:57
Avant toute démarche je définis soigneusement mes notations :
qα : Charge de la particule α
V(A), V(B) potentiels électriques en A et B
vA, vB vitesses de la particule α en A et B
mα : masse de la particule α
Energie mécanique en A : Em(A) = Ec(A) + Ep(A)
Energie mécanique en B : Em(B) = Ec(B) + Ep(B)
Conservation de l'énergie mécanique : Em(A) = Em(B)
l'énoncé dit : vA = 0 ce qui implique Ec(A)=0
donc 0 + qα VA = (1/2) mα(vB)² + qα V(B)
Je te laisse terminer ….
Rien à faire pour te convaincre !
Tu notes encore le potentiel électrique en B de la même manière que la vitesse en B
Calculer la valeur V(A)-V(B)
V(A)-V(B)=6,70×10^-27*1,00×10^5/2×3,12×10^-19
V(A)-V(B)= 6,7×10^-22/6,24×10^-19
V(A)-V(B)=1,07×10^-6 V
Attention tu confonds les verbes "excuser" et "accuser"
Telle que tu l'as écrite, l'expression de V(A)-V(B) que tu as obtenue est évidemment fausse .
Voici l'expression exacte :
Ton résultat numérique est invraisemblable puisque voisin de un millionième de volt !
L'erreur semble provenir de la vitesse de la particule alpha
Tu inverses les rôles.
C'est à toi de proposer un résultat.
De plus, il se trouve que je n'ai pas encore fait le calcul.
Après avoir remarqué l'invraisemblance du résultat, il m'a semblé que ton erreur provenait de la vitesse.
Bonsoir
Avant de proposer un résultat je vais convertir la vitesse en m
m/s
1,00×10^3 km/s=1,00×10^5 m/s
V(A)-V(B)= 6,70×10^-27*1,00×10^5/2×3,12×10^-19
V(A)-V(B)=6,7×10^-22,/6,24×10^-19
V(A)-V(B)=1,07×10^-41 V
Ce résultat est encore plus invraisemblable que le précédent.
1 km = 103 m
1 km/s = 103 m/s
103 km/s = 103 *103 = 106 m/s
Indication : Le résultat est de l'ordre de plusieurs milliers de volts.
Bonjour
C est mon tour de vous donnez le bon résultat
V(A)-V(B)=6,7×10^-27×(1,00×10^6)^2/(3,2×10^-19)
V(A)-V(B)=6,7×10^-15/3,2×10^-19
V(A)-V(B)=2,1×10^-34 V
Tu es décidément fâché avec les ordres de grandeur.
Mon indice disait : "Plusieurs milliers de volts"
Ton résultat est de l'ordre du dix millionième de milliardième de milliardième de milliardième de volt.


