Inscription / Connexion Nouveau Sujet
énergie potentielle électrostatique
Bonjour
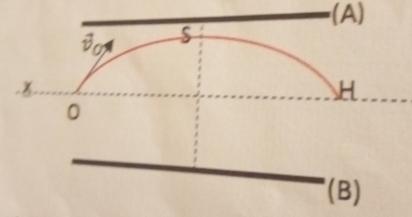
Tu considéré un électron lancé a la vitesse Vo . il pénètre en o entre deux plaque parallèle A et B où régné un champ électrique uniforme . la vitesse Vo fait avec l axé x'x parallèle aux plaque , un angle a et V0 =6,10^6 m/s . la trajectoire de l électron entre les plaques est un arc de parabole de sommet S.
1/ indique en justifiant ta réponse la plaque chargée positivement et celle chargée négativement
Comme le champ est uniforme alors la plaque chargee positivement et celle chargée négativement
2 montre que la vitesse VH de sortie de l électron est égale a VO
Je ne sais pas quelle méthode utilisée
Bonjour,
Comme le champ est uniforme alors la plaque chargee positivement et celle chargée négativemen
Cette phrase ne veut rien dire.
On te demande de trouver en le justifiant laquelle (A ou B) des plaques est chargée positivement et laquelle est chargée négativement.
Question 2 : La méthode la plus simple est d'appliquer à l'électron la conservation de l'énergie mécanique.
Salut
Comment justifie laquelle ( A et B) qui chargée positivement et celle négativement
2 / appliquons la conservation de l énergie mécanique entre o et H
Em(o)=Em(H)
1/2 mv^2o =1/2mV^2 H
V^2o=.V^2H
Donc Vo=VH
VH=6,10^6,m/s
Le signe des charges électriques portées par A et par B se déduit de la trajectoire de l'électron telle qu'elle est représentée sur la figure.
L'énergie mécanique est égale à la somme de l'énergie cinétique et de l'énergie potentielle potentielle électrique.
Tu as tout simplement ignoré l'énergie potentielle potentielle électrique !
Non.
L'électron a une vitesse initiale dirigée vers la plaque A
S'il était attiré par la plaque A, sa trajectoire ne s'incurverait pas vers la plaque B.
L'électron est attiré par la plaque B qui est donc la plaque électrisée positivement.
Tu peux comparer cela à une pierre lancée obliquement vers le haut, mais qui finit par retomber car elle est attirée par la Terre vers le bas.
Bonjour
Ok
Donc la plaque A est charge négativement
2
Em(A)=Em(B)
1/2 mV^2 A + EpA= 1/2 mV^2 + EpB
1/2 mV^2 A + qvA +cte= 1/2 mV^2 + qB + cte
Je suis bloqué
L'énergie potentielle est (en principe) la somme de deux énergies potentielles :
- L'énergie potentielle de pesanteur.
- L'énergie potentielle électrique.
Le poids de l'électron étant négligeable devant la force électrique on prendra uniquement en considération l'énergie potentielle électrique.
A toi d'exprimer cette énergie potentielle électrique et de l'utiliser dans la conservation de l'énergie mécanique.
Je vous comprends mais je n arrive pas a faire le calcul
Peux tu me montre le début du calxul. Pour je puisse comprendre
Energie potentielle électrique en O :
Ep(O) = qVO + k
Energie mécanique en O :
Em(O) = Ec(O) + Ep(O) = Ec(O) + qVO + K
Fais la même chose en A, puis applique la conservation de l'énergie mécanique
Bonjour
Énergie électrique en H au lieu de A
Ep(H)= qVH +k
Énergie mécanique en H
Em(H)=Ec(H)+Ep(H)=EC(H)+ qVH +k
Appliquons la conservation de l énergie mécanique entre o et H
Em(o)=Em,(H)
EC(o)+ qVo +k = EC(H)+qVH+k
EC(o)+qVo=EC(H)+ qVH
1/2 mV^2o+qVo = 1/2 mV^2H+qVH
1/2 mV^2o-1/2mV^2H=qVH-qVo
1/2 m(V^2o-V^2H)=q(VH-Vo)
J ai besoin de votre aide pour le reste du calcul
Il est inutile d'alourdir le calcul en explicitant dès à présent l'énergie cinétique.
On a donc :
Em(O) = Ec(O) + Ep(O) = Ec(O) + qVO + K
Em(H) = Ec(H) + Ep(H) = Ec(H) + qVH + K
Conservation de l'énergie mécanique :
Em(O) = Em(H)
Ce qui donne après simplification :
Ec(O) - Ec(H) = q (VH - VO)
On constate que si on réussit à démontrer que les potentiels électriques de O et de H sont égaux cela impliquera que les énergies cinétiques, donc aussi les vitesses en ces points sont égales.
Désolé, mais je ne comprends pas ce que tu as voulu dire.
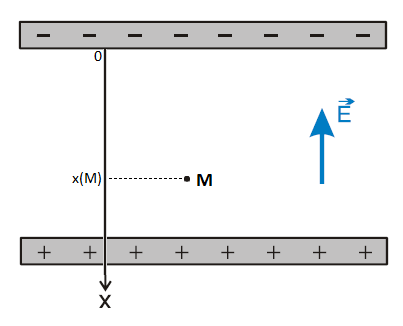
Le potentiel électrique d'un point M situé dans un champ électrique uniforme dépend de la valeur de ce champ et de la position du point.
Si on choisit la plaque A pour origine des potentiels alors le potentiel électrique VM du point M est :
VM = E * x(M)
La suite :
x(O) = x(H)
donc V(O= = V(H)
V(H) - V(O) = 0
donc Ec(O) = Ec(H)
Ayant la même énergie cinétique en O et en H l'électron a aussi la même vitesse.


