Bonjour

extrait de la FAQ du forum :

Q01 - Que dois-je faire avant de poster une question ?

Plusieurs choses sont à faire avant d'envisager de poser une question sur le forum.

Tout d'abord, réellement chercher à résoudre seul votre problème. En effet, le but du forum n'est pas de faire les exercices à votre place.

Cherchez également si votre question n'a pas déjà été posée sur le forum. Pour cela vous pouvez utiliser le moteur de recherche (en panne pour le moment) ou le net en tapant quelques mots clés, par exemple, le début de votre énoncé.

Vous pouvez aussi parcourir le forum en choisissant une classe spécifique (de la sixième au supérieur) dans la page de choix du forum. Vous trouverez certainement un exercice déjà posté et corrigé qui ressemblera fortement au vôtre.

Enfin, vous pouvez également consulter les fiches du site se rapportant à votre chapitre. Parfois une simple relecture de celles-ci vous permettra de vous rappeler d'une définition, d'une propriété, d'une condition d'application d'une loi (données, hypothèses, ...), d'une méthode oubliée, etc.

Somme toute, n'envoyez pas le sujet d'un exercice sans montrer que vous y avez travaillé sérieusement.

1) Ep=-W(T)

Bonsoir,

Pas clair tout ça !
Le titre du topic parle d'énergie potentielle élastique, mais l'énoncé n'évoque que de l'énergie potentielle de pesanteur.

Ta participation se limite à une "formule" dont on ignore la signification. Tu ne t'es pas beaucoup fatigué ....

Et si tu prenais les choses dans l'ordre de l'énoncé en postant pour commencer le résultat de tes recherches concernant les question 1 et 2 ?

Bonjour

1) le travail W(T) de la tension = - le travail W(P) du poids.

W(T)=-W(P).

2) on a Ep₀=mg(l-lo). (Ep: l'énergie potentielle , m la masse).

Or Ep₀=0 J

Donc mg(l-lo)=0


0=mg(l-lo)

mgl-mglo=0

mgl=mglo

l=lo

l=0,6m

Question 1 :

Comme tu le sais probablement, calculer le travail d'une force suppose que celle ci se déplace.
Ici la sphère est en équilibre : Aucune des deux forces qui s'exerce sur elle ne se déplace donc aucune des deux ne travaille.
De plus, la question demande une relation entre T et P et non entre et  

La bonne méthode consiste à appliquer une des lois  bien connues de la physique au sujet de l'équilibre de la sphère. (Préciser quelle est cette loi)

Bonjour , quelle loi ?

Lorsque un corps est en équilibre sous l'action de deux forces celles ci sont opposées.
Elles ont donc même direction, sens contraire et même intensité.

Pour en savoir plus :

D'accord donc ici

D'où

Oui, c'est exact mais cela ne répond pas exactement à la question posée.
En effet, on ne te demande pas une relation entre   et  , on te demande une relation entre T et P

Bonsoir , dans ce cas T=P

Exactement !

Question 2 :
Tu trouves donc que le ressort garde la même longueur qu'on lui accroche ou non la sphère.
Un peu étonnant non ?
Laisse tomber l'énergie potentielle pour cette question et concentre toi plutôt sur la loi de Hooke concernant les ressorts.

La question 2 maintenant .

2) J'ai essayé ...

Ah message croisé , donc vous me conseillez de laisser tomber l'énergie potentielle élastique ...

Pourquoi ??


Mon cours porte sur cette leçon pourtant .

Tu trouves donc que le ressort garde la même longueur qu'on lui accroche ou non la sphère.
Un peu étonnant non? effectivement

Ok , d'après la loi de Hook , T=k×∆l , k: raideur , ∆l : allongement.

On sait que T=P or P=0,5×9,8=4,9N

D'où T=4,9N.

Donc 4,9=40×∆l

∆l=≈0,12m

l=0,12m.

Décidément tu as un faible pour les résultats invraisemblables.
Voilà donc un ressort de longueur 60cm, on lui accroche une sphère de masse 500g et sa longueur devient égale à 12 cm.

Pourtant tu as employé une méthode correcte.
Je te laisse réfléchir .....

Euh oui , comment faire pour ne plus passer pour çà ?

Alors j'avais pas vu le lo.

D'après Hooke ,

T=k×∆l

T=k×(l-lo)

4,9=40×(l-0,6)

l=≈0,72m

l=72cm .

En effet :
L = L₀ + mg / k = 0,60 + (0,5 * 9,8) / 40 0,72m

Conclusion : Penser à vérifier, lorsque c'est possible, la vraisemblance d'un résultat.

Conclusion : Penser à vérifier, lorsque c'est possible, la vraisemblance d'un résultat. Mais comment ??

3) Maintenant , comment faire ?

Un ressort qui ne s'allonge pas  ou qui raccourcit quand on lui accroche une masse cela devrait immédiatement attirer l'attention.
On peut multiplier les exemples à l'infini :

Parmi ceux déjà rencontrés par ailleurs :
Une distance Terre - Lune de 384 km
Un courant électrique de 50 mA pour alimenter le moteur d'un TGV
etc ...

Question 3 : Appliquer les règles de calcul concernant l'énergie potentielle de pesanteur.

Ok

Énergie potentielle élastique non ?

∆Ep=

Donc Ep_A-Ep_B=


Or Ep_A=0J

Donc -Ep_B=

Ep_B=-()

Ep_B=-(=-0,8J

Retour à l'énoncé :
3) Déterminer l'énergie potentielle du système (sphère+support) dans le champ de pesanteur, lorsqu'il est écarté de x=0,2m de sa position d'équilibre.

La question ne porte pas sur l'énergie potentielle élastique, mais sur l'énergie potentielle de pesanteur.

Bonjour ,

Donc Ep_p=mg(za-zb)

Or za=0

D'où Ep_p=mg(-zb)

Zb=x=0,2m

Ep_p=0,5×9,8×(-0,2)

Ep_p=-0,98J

Ton résultat numérique est exact, mais la justification n'est pas claire.

On définit l'énergie potentielle de pesanteur à partir de sa variation :
ΔE_pp = m * g *  Δz

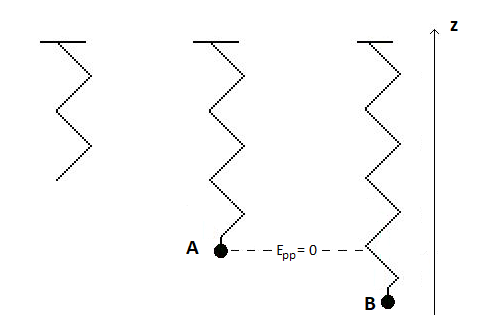
ce qui donne ici :  E_pp(B) - E_pp(A) = m * g * (z_B - z_A)  (relation 1)

L'énoncé impose Epp(A) = 0
Sur l'axe Oz (Voir figure) je choisis, pour simplifier, l'origine des altitudes au point A
donc z(A) = 0
La relation (1) devient : E_pp(B) = m * g * z_B

Application numérique :
E_pp(B) = 0,5 * 9,8 * (-0,2) = - 0,98J

D'accord , merci .