Inscription / Connexion Nouveau Sujet
Énergie potentielle de pesanteur
Bonjour tout le monde, j'ai besoin d'aide pour cet excercice :
Une petite sphère métallique supposée ponctuelle de masse m=120g est suspendue à un fil inextensible et de masse négligeable, de longueur L=70cm. L'extrémité du fil est accroché en un point O. On écarte le pendule ainsi constitué de la verticale, selon un angle de 25°.
1- Calculer l'énergie potentielle de pesanteur Ep,p(A) de la sphère dans cette position en prenant la position d'équilibre comme position de référence.
2- On voudrait lâcher ce pendule depuis une position B d'énergie potentielle de pesanteur Ep,p(B)=2Ep,p(A). Calculer l'angle que ferait alors le fil tendu avec la verticale.
Hello
1) Peux tu regarder dans ton cours la définition de l'énergie de pesanteur?
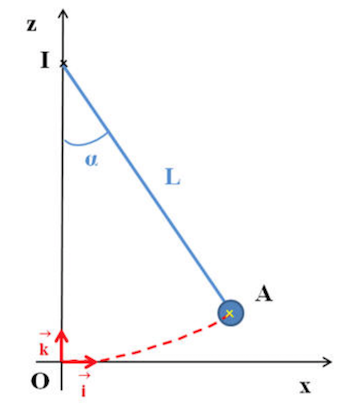
2) Peux tu, en utilisant le schéma ci dessous), exprimer la coordonnée z(A) en fonction de 
La résolution du problème devrait alors ne plus te poser de problème ... ? 
Donc voila comment j'ai procédé :
Ep,p(A) = m.g.L.sin25
= 0.12 x 9,8 x 0.7 x sin25
Ce qui donne : -0.108 J
Tu vois que j'avais raison de m'inquiéter
Ce qui donne : -0.108 J
Le signe moins il sort d'où ?
Et le point B? son angle vaut?
Est-ce-que l'expression littérale est juste car quand je refais le calcul la reponse est toujours négative ?
1) Peux tu regarder dans ton cours la définition de l'énergie de pesanteur?
2) Peux tu, en utilisant le schéma ci dessous), exprimer la coordonnée z(A) en fonction de
1)
Ici, l'énoncé te dit de prendre comme origine de l'énergie potentielle l'altitude du point O
Donc ici
2)
)
PS: tu contrôleras également l'unité d'angle de ta calculette (qui je crois est positionnée sur "radians")
Merci beaucoup et tu as raison a propos de ma calculette.
Pour la deuxieme question j'ai fait :
Ep,p(B)= 2Ep,p(A)
m.g.L(1-cos b) = 2 m.g.L(1-cos25)
Ce qui nous donne cos b =0.81
Donc l'angle est egal a 35°
J'espere que cette fois-ci c'est juste 
cos
= 2cos
35° 
je n'aurais rien pu faire
Si, si tu aurais pu faire des ... erreurs
(avec moi aussi d'ailleurs, ça arrive)
Annuler
connectez vous