Inscription / Connexion Nouveau Sujet
énergie potentielle
Salut
L exercice me semble bizarre
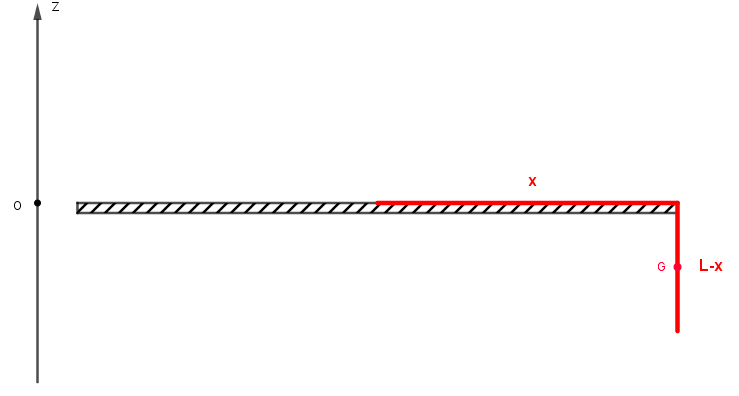
Au cours d une séance de TP cours , tu est désigné par le professeur pour étudier le mouvement d une chaine. La chaîne AB de longueur l=1m et de masse mo=100 g repose sur le bord d une table
Une portion de la chaîne quitte la table.la longueur de la chaîne encore sur la table est x
Données la masse de la chaîne est proportionnelle a sa longueur
La surface supérieure de la table est le niveau de référence pour l énergie potentielle de pesanteur
Ainsi que l origine des altitudes g=10N/kg
1_ exprime
1_2/ la masse m de la portion ayant quitté la table en fonction de mo l et x
1_2/ l altitude du centre d inertie G de la portion ayant quitté la table
2
2_1/déduis en l expression littérale de l énergie potentielle de pesanteur de la. Chaîne
2_2/ calcule la valeur de cette énergie lorsque la moitié de la chaîne a quitté la table.
Bonjour
1_2) m=((l-x)/l)mo
1_2) z(G)=-(l-x)/2
2_1) Epp=mgz=g((l-x)/l)mo*[-(l-x)/2]
2_2) faites l'application numerique avec x=l/2. Vous avez tout.
Bonne chance
Bonsoir
IL y a l un de mes amis qui m a pose la question
Comment tu as trouvé les formules ?je ne sais pas comment le réponse
Aide moi s il vous plait
Bonjour,
En l'absence de Sayef et d'odbugt1 (que je salue  ), une indication supplémentaire :
), une indication supplémentaire :
* l'altitude de référence z = 0 pour ton exercice correspond à la position de la table par rapport à l'axe (Oz).
* Ainsi toute la portion de la chaîne (d'après le schéma, de longueur x) n'est pas soumise à une énergie potentielle de pesanteur (Epp = m.g.z = 0 J puisque z = 0), il faut donc étudier la portion de circuit (l-x) qui n'est plus en repos sur la table et qui est soumise à une énergie potentielle de pesanteur.
* La première étape consiste donc à exprimer la masse m de cette portion de chaîne hors de la table et de se souvenir que le point G est au centre de cette portion de circuit hors de la table.
A toi désormais d'essayer d'aboutir aux mêmes résultats que Sayef ...

Voici ma réponse
Puis l énoncé dit la masse de la chaine est proportionnelle a sa longueur donc on
mo/l=m/(l-x)
m ×l=mo × (l-x)
m=mo(l-x)/l
Oui ! Ce qui est cohérent avec le résultat de Sayef :
- si x = 0, alors m = mo => toute la chaîne a quitté la table ;
- si x = l, alors m = 0 => toute la chaîne repose sur la table.
C'était la question la plus difficile de l'exercice, le reste découle du cours et du schéma d'odbugt1.

On considère que le champ de pesanteur est uniforme par hypothèse (puisque g = 10 N/kg = constante d'après l'énoncé).
On peut donc considérer que le centre d'inertie est confondu avec le centre de gravité de la portion de chaînette suspendue : celle-ci faisant une longueur (l-x), alors zg = -(l-x)/2
Remarque : le signe "-" est par rapport au repère (Oz) défini sur le schéma.